Question

在平面直角坐标系中，若P，Q满足条件：（1）P，Q都在函数f（x）的图象上；（2）P，Q两点关于直线y=x对称，则称点对{P，Q}是函数f（x）的一对“可交换点对”．（{P，Q}与{Q，P}看作同一“可交换点”）．试问函数f（x）=

x2+3x+2(x≤0) log2x(x＞0)

的“可交换点对有（　　）

Answer 1

分析：根据“可交换点”的定义作出f（x）=log₂x（x＞0）关于直线y=x对称的图象C，判断C与函数f（x）=x²+3x+2（x≤0）的图象交点个数，可得答案．

解答：解：∵f（x）=log₂x（x＞0）关于直线y=x对称的图象C：y=2^x，
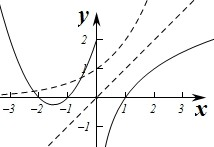
作出函数y=2^x与函数f（x）=x²+3x+2（x≤0）的图象如图：
由图象可知两个函数的图象有2个不同交点，
∴函数的“可交换点对”有2对．

故选C．

点评：本题考查的知识点是函数零点个数及判断，数形结合思想是解答本题的关键，而解答的核心在于将问题转化为函数图象的交点个数问题．