题目内容
(本小题满分12分)已知直线x-2y+2=0经过椭圆C: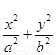 =1(
=1(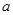 >
>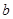 >0)的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方
>0)的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方
的动点,直线AS、BS与直线l:x=分别交于M、N两点.
(1)求椭圆C的方程;
(2)求线段MN的长度的最小值;
(3)当线段MN的长度最小时,在椭圆C上是否存在这样的点T,使得△TSB的面积为?若存在,确定点T的个数,若不存在,说明理由.
(1)+y2=1
(2)
(3)当线段MN的长度最小时,椭圆上仅存在两个不同的点T,使△TSB的面积为
【解析】解析:(1)由已知得,椭圆C的左顶点为A(-2,0),上顶点为D(0,1),
∴a=2,b=1,故椭圆C的方程为+y2=1………..4分
(2)直线AS的斜率k显然存在,且k>0,故可设直线AS的方程为y=k(x+2),从而M,
由得(1+4k2)x2+16k2x+16k2-4=0.
设S(x1,y1),则(-2)·x1=得x1=,
从而y1=,
即S,又B(2,0),
由得,
∴N,
故|MN|=,
又k>0,∴|MN|=+≥2=.
当且仅当=,即k=时等号成立.
∴k=时,线段MN的长度取最小值………8分
(3)由(2)可知,当MN取最小值时,k=,
此时BS的方程为x+y-2=0,S,∴|BS|=,
要使椭圆C上存在点T,使得△TSB的面积等于,只需T到直线BS的距离等于,
所以T在平行于BS且与BS距离等于的直线l上.
设直线l′:x+y+t=0,
则由=,解得t=-或t=-.
①当t=-时,由得5x2-12x+5=0,
由于Δ=44>0,故l′与椭圆C有两个不同的支点;
②当t=-时,由得5x2-20x+21=0,
由于Δ=-20<0,故直线l′与椭圆没有交点.
综上所述,当线段MN的长度最小时,椭圆上仅存在两个不同的点T,使△TSB的面积为………12分

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案