题目内容
函数 的定义域为A,若
的定义域为A,若 且
且 时总有
时总有 ,则称
,则称 为单函数.例如,函数
为单函数.例如,函数 是单函数.下列命题:
是单函数.下列命题:
①函数 是单函数;
是单函数;
②函数 是单函数;
是单函数;
③若 为单函数,
为单函数,  且
且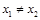 ,则
,则 ;
;
④若函数 在定义域内某个区间D上具有单调性,则
在定义域内某个区间D上具有单调性,则 一定是单函数.
一定是单函数.
其中真命题是 (写出所有真命题的编号).
③
解析试题分析:解:①令 得:
得: ,所以,
,所以, ,
,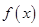 不是单函数;
不是单函数;
②因为 ,所以
,所以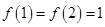 ,故
,故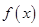 不是单函数;
不是单函数;
③与定义是互为逆否命题,是真命题
根据①和②知:若函数 在定义域内某个区间D上具有单调性,则
在定义域内某个区间D上具有单调性,则 不一定是单函数.所以④是假命题.
不一定是单函数.所以④是假命题.
综上真命题只有: ③;故答案应填③
考点:1、函数的概念;2、新定义;3、函数的单调性;4、分段函数.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 上的函数
上的函数 满足:①当
满足:①当 时,
时, ②
② ,设关于
,设关于 的函数
的函数 的零点从小到大依次记为
的零点从小到大依次记为 ,则
,则 ________.
________.
 ,若函数
,若函数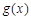 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数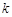 的取值范围为 .
的取值范围为 .
 ,若函数
,若函数 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数 的取值范围为 .
的取值范围为 . 是奇函数,且在
是奇函数,且在 内是减函数,又
内是减函数,又 ,则
,则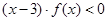 的解集是
的解集是  ,若
,若 ,那么
,那么 ______
______ 在
在 上的最大值为p,最小值为q,则p+q=
上的最大值为p,最小值为q,则p+q=  的值域为____________.
的值域为____________.