题目内容
(本题满分13分)已知椭圆 的左焦点
的左焦点 的坐标为
的坐标为 ,
, 是它的右焦点,点
是它的右焦点,点 是椭圆
是椭圆 上一点,
上一点,  的周长等于
的周长等于 .
.
(1)求椭圆 的方程;
的方程;
(2)过定点 作直线
作直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,且
,且 (其中
(其中 为坐标原点),求直线
为坐标原点),求直线 的方程.
的方程.
【答案】
(1)  (2)
(2)  和
和
【解析】
试题分析:(1)由已知得 所以椭圆
所以椭圆 的方程为
的方程为 .
(5分)
.
(5分)
(2)显然直线 不符合条件,故设直线
不符合条件,故设直线 的方程为
的方程为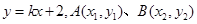 (6分)
(6分)
由
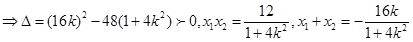 ……(*)
(8分)
……(*)
(8分)
由
 (10分)
(10分)
将(*)式代入得 解得
解得
当 时,
时, 
故所求直线 有两条,其方程为
有两条,其方程为 和
和 (13分)
(13分)
考点:直线与椭圆的位置关系
点评:解决该试题的关键是熟练的运用其性质得到其方程,并结合设而不求的思想来结合韦达定理得到系数与根的关系,进而得到求解,属于中档题。

练习册系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.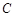 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.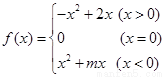 为奇函数;
为奇函数;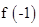 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆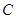 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.