题目内容
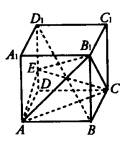
如图,已知正四棱柱ABCD—A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB =a.
(1) 求截面EAC的面积;
(2) 求异面直线A1B1与AC之间的距离;
(3) 求三棱锥B1—EAC的体积.
答案:
解析:
解析:
| 解:(1)
连DB交AC于O,连EO.
∵ 底面ABCD是正方形, ∴ DO⊥AC. 又∵ ED⊥底面AC, ∴ EO⊥AC. ∴∠EOD是面EAC与底面AC所成二面角的平面角. ∴ ∠EOD =45°,
(2) 易知A1A 是异面直线A1 B1与AC的公垂线段. ∵ D1B∥面EAC. ∴ D1B∥EO, 又O是DB中点,E是D1D中点,D1B =2EO =2a. ∴ 异面直线A1 B1与AC间的距离为 (3) 连结D1B1. ∵ 连结B1D交D1 B于P,交EO于Q, ∵ B1D⊥D1 B,EO∥D1B1. ∴ B1D⊥EO. 又AC⊥EO,AC⊥ED. ∴ AC⊥面BDD1 B1, ∴ B1D⊥AC ∴ B1D⊥面EAC. ∴ B1Q是三棱锥B1-EAC的高. ∴ 所以三棱锥B1-EAC的体积是
|

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a. 如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.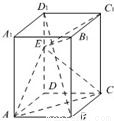 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.