题目内容
四棱锥S-ABCD中，底面ABCD为矩形，∠SCD=90°，∠SBC=90°，二面角S-CD-B为60°，且AB=SC=4．
（1）求证：平面SAB⊥平面ABCD；
（2）求三棱锥C-ASD的高（即以△SAD为底的三棱锥的高）．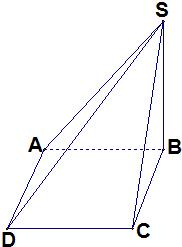
（1）求证：平面SAB⊥平面ABCD；
（2）求三棱锥C-ASD的高（即以△SAD为底的三棱锥的高）．
（1）证明：
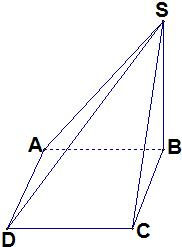
∵DC⊥BCDC⊥SC∴DC⊥平面SCB
∴DC⊥SB且∠SCB为二面角S-CD-B的平面角，则∠SCB=60°
又∵SB⊥BC∴SB⊥平面ABCD
又∵SB?平面SAB∴平面SAB⊥平面ABCD
（2）连接AC
∵SB⊥平面ABCD∴SB⊥AD又AD⊥AB
∴AD⊥平面SAB∴AD⊥SA
在Rt△ASD1中AS=
=
=2
，AD=BC=2
由VC-SAD=VS-ACD∴AD×AS•h=AD×CD×SB
∴h=
∴三棱锥C-ASD的高为
∵DC⊥BCDC⊥SC∴DC⊥平面SCB
∴DC⊥SB且∠SCB为二面角S-CD-B的平面角，则∠SCB=60°
又∵SB⊥BC∴SB⊥平面ABCD
又∵SB?平面SAB∴平面SAB⊥平面ABCD
（2）连接AC
∵SB⊥平面ABCD∴SB⊥AD又AD⊥AB
∴AD⊥平面SAB∴AD⊥SA
在Rt△ASD1中AS=
| AB2+SB2 |
42+(2
|
| 7 |
由VC-SAD=VS-ACD∴AD×AS•h=AD×CD×SB
∴h=
4
| ||
| 7 |
4
| ||
| 7 |
练习册系列答案
阅读快车系列答案
相关题目
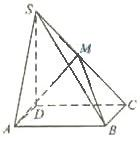如图，四棱锥S-ABCD中，底面ABCD为矩形，SD⊥底面ABCD，AD=
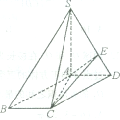如图，在四棱锥S-ABCD中，底面ABCD为平行四边形，SA⊥平面ABCD，AB=2，AD=1，
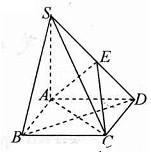如图，在底面是菱形的四棱锥S-ABCD中，SA=AB=2，SB=SD=2
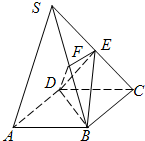如图，在四棱锥S-ABCD中，底面ABCD为正方形，侧棱SD⊥底面ABCD，SD=AD，DF⊥SB垂足为F，E是SD的中点．