题目内容
已知
a、b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是[ ]
|
A .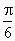 |
B .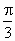 |
|
C .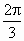 |
D .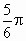 |
答案:略
解析:
解析:
|
解:∵ (a-2b)⊥a,∴ (a-2b)·a=0,即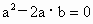 .① .①
∵ (b-2a)⊥b,∴ (a-2a)·b=0,即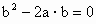 .② .②
由①②知 |a|=|b|.∴ 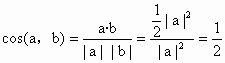 . .
∴ 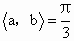 . .
求 a与b的夹角,首先求夹角的余角的余弦值,然后根据范围,求出夹角.本题主要考查向量的数量积、向量的夹角、向量垂直的条件. |

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知
,
是非零向量,满足
=λ
,
=λ
(λ∈R),则λ=( )
| a |
| b |
| a |
| b |
| b |
| a |
| A、-1 | B、±1 | C、0 | D、0 |