题目内容
设函数y=sinx的定义域为[a,b],值域为[-1,
],则以下结论中错误的是( )
| 1 |
| 2 |
分析:作出正弦函数 y=sinx的图象,并加以观察,并根据函数的单调性对A、B、C、D各项的结论进行推理论证,结合取特殊的a、b值检验,可得A、B、C都正确,而D项错误,由此得到答案.
解答:解:作出正弦函数 y=sinx的图象,加以观察得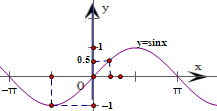
对于A,当a=-
且b=
时,函数在区间[a,b]上单调增,
可得函数的最小值为sin(-
)=-1;函数的最大值为sin
=
此时函数的值域为[-1,
],b-a的达到最小值
,故A正确;.
对于B,当a=-
且b=
时,函数在区间[a,b]上先单调递减,
再单调递增,
函数的最小值为sin(-
)=-1;且最大值为sin(-
)=sin
=
,
此时函数的值域为[-1,
],b-a的达到最大值
,故B正确;.
对于C,如果a=2kπ-
(k∈Z),由于sina=-
没有达到最小值1,则b≥2kπ+
才能出现函数的最小值1,而此时函数的最大值为1而不是
,与题设矛盾
因此a不可能等于2kπ-
(k∈Z),可得C正确;
对于D,当a=-
且b=-
时,根据函数图象可得函数的值域为[-1,
],
说明b值可能等于2kπ-
(k∈Z),故D不正确
故选:D

对于A,当a=-
| π |
| 2 |
| π |
| 6 |
可得函数的最小值为sin(-
| π |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
此时函数的值域为[-1,
| 1 |
| 2 |
| 2π |
| 3 |
对于B,当a=-
| 7π |
| 6 |
| π |
| 6 |
再单调递增,
函数的最小值为sin(-
| π |
| 2 |
| 7π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
此时函数的值域为[-1,
| 1 |
| 2 |
| 4π |
| 3 |
对于C,如果a=2kπ-
| π |
| 6 |
| 1 |
| 2 |
| 3π |
| 2 |
才能出现函数的最小值1,而此时函数的最大值为1而不是
| 1 |
| 2 |
因此a不可能等于2kπ-
| π |
| 6 |
对于D,当a=-
| 7π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
说明b值可能等于2kπ-
| π |
| 6 |
故选:D
点评:本题给出正弦函数的几个结论,要求找出其中的假命题,考查了正弦函数的图象与性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,给出以下四个结论:
,给出以下四个结论:

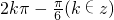
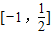 ,给出以下四个结论:
,给出以下四个结论: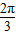
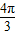
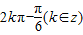
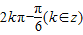 其中正确的有( )
其中正确的有( )