题目内容
设函数y=sinx的定义域为[a,b],值域为[-1,
],给出以下四个结论:
①b-a的最小值为
②b-a的最大值为
③a不可能等于2kπ-
(k∈z)
④b不可能等于2kπ-
(k∈z)其中正确的有( )
| 1 |
| 2 |
①b-a的最小值为
| 2π |
| 3 |
②b-a的最大值为
| 4π |
| 3 |
③a不可能等于2kπ-
| π |
| 6 |
④b不可能等于2kπ-
| π |
| 6 |
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:画出函数的图象,利用函数的值域,推出函数的定义域的范围,然后求出a,b与b-a的值的情况,即可得到结果.
解答:解:函数y=sinx的定义域为[a,b],∵值域为 [-1,
]
由y=sinx的图象
b-a的最大值为
-(-
)=
;
最小值为
-(-
)=
;
∴|
+2kπ|≤b-a≤|
+2kπ|(k∈z),
当k=0或-1时,则可能为B和D中的值,
由正弦曲线知,当a=
,b=
时,也满足条件.
①b-a的最小值为
,正确;
②b-a的最大值为
,正确
③a不可能等于2kπ-
(k∈z)正确;
④b不可能等于2kπ-
(k∈z)错误 .
.
故选C.
| 1 |
| 2 |
由y=sinx的图象
b-a的最大值为
| π |
| 6 |
| 7π |
| 6 |
| 4π |
| 3 |
最小值为
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
∴|
| 2π |
| 3 |
| 4π |
| 3 |
当k=0或-1时,则可能为B和D中的值,
由正弦曲线知,当a=
| 5π |
| 6 |
| 11π |
| 6 |
①b-a的最小值为
| 2π |
| 3 |
②b-a的最大值为
| 4π |
| 3 |
③a不可能等于2kπ-
| π |
| 6 |
④b不可能等于2kπ-
| π |
| 6 |
 .
.故选C.
点评:本题是基础题,考查三角函数的图象的应用,考查函数的定义域,考查计算能力,转化思想.

练习册系列答案
相关题目
 ,给出以下四个结论:
,给出以下四个结论:

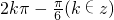
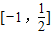 ,给出以下四个结论:
,给出以下四个结论: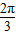
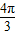
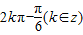
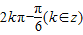 其中正确的有( )
其中正确的有( )