题目内容
(本题10分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点,将△ACD沿 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
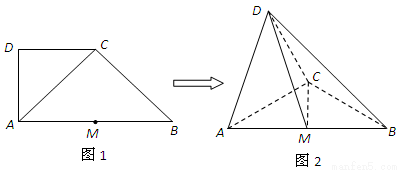
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求二面角A-CD-M的余弦值.
【答案】
(Ⅰ)见解析;(Ⅱ)cos∠MNO= =
=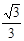 。
。
【解析】(I) 取AC的中点O,连接DO,则DO⊥AC,因为平面ACD⊥平面ABC,所以DO⊥平面ABC,∴DO⊥BC,可得易证: ,从而可证出BC⊥平面ACD;
,从而可证出BC⊥平面ACD;
(II)找(或做)出二面角的平面角.取CD的中点N,连接MO, NO, MN,则MO∥BC,
∴MO⊥平面ACD,∴MO⊥CD,∵AD⊥CD,ON∥AD,∴ON⊥CD,又∵MO∩NO=O,
∴CD⊥平面MON,∴CD⊥MN,∴∠MNO是所求二面角的平面角.

解:(Ⅰ)取AC的中点O,连接DO,则DO⊥AC,
∵平面ADC⊥平面ABC,∴DO⊥平面ABC,∴DO⊥BC,………2分
在直角梯形ABCD中,连接CM,可得CM=AD=2,AC=BC=2 ,
,
∴AC2+BC2=AB2,∴AC⊥BC,
又∵DO∩AC=O,∴BC⊥平面ACD;………………………………3分
(Ⅱ)取CD的中点N,连接MO, NO, MN,
则MO∥BC,∴MO⊥平面ACD,∴MO⊥CD,……………………1分
∵AD⊥CD,ON∥AD,∴ON⊥CD,又∵MO∩NO=O,
∴CD⊥平面MON,∴CD⊥MN,∴∠MNO是所求二面角的平面角…2分
在Rt△MON中,MO= =
= ,NO=
,NO= =1,
=1,
∴MN= =
= ,∴cos∠MNO=
,∴cos∠MNO= =
=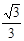 ………………2分
………………2分

练习册系列答案
相关题目
 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛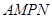 ,要求
,要求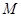 在
在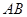 的延长线上,
的延长线上,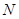 在
在 的延长线上,且对角线
的延长线上,且对角线 过
过 点.已知
点.已知 米,
米,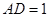 米.
米. (单位:米),要使花坛
(单位:米),要使花坛 的取值范围;
的取值范围;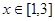 (单位:米),则当
(单位:米),则当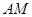 ,
,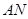 的长度分别是多少时,花坛
的长度分别是多少时,花坛
 如图,
如图,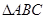 内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且
内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且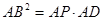

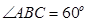 ,⊙O的半径为1,
,⊙O的半径为1, 为弧
为弧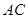 的中点,求
的中点,求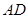 的长。
的长。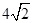 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?