题目内容

12．等比数列{an}中，若a1+a2+a3=7，a4+a5+a6=56，求a7+a8+a9的值．

分析 由等比数列的性质可得，a4+a5+a6=（a1+a2+a3）q3，可求7q3，而a7+a8+a9=（a4+a5+a6）q3，可求

解答 解：设等比数列{an}的公比为q，
则a4+a5+a6=（a1+a2+a3）q3，
∴56=7q3，
解得q3=8，
∴a7+a8+a9=（a4+a5+a6）q3=56×8=448，
故选：C．

点评 本题考查等比数列的性质和通项公式，属基础题．

练习册系列答案
相关题目
2．在平面直线坐标系xOy中，给定一点P（3，1）及两条直线l1：x+2y+3=0，l2：x+2y-7=0．
（Ⅰ）求直线l1和l2距离相等的直线方程；
（Ⅱ）求过P点且与l1，l2都相切的圆的方程．
3．已知在△ABC中，角A，B，C对边分别是a，b，c，若B为钝角，且$\frac{1}{sinA}+\frac{1}{cosA}=2\sqrt{2}$．
（Ⅰ） 求角A；
（Ⅱ） 若$\overrightarrow{AB}•\overrightarrow{AC}=3$，且$a=\sqrt{5}$，求b和c的值．
20．已知不等式ax2+bx+4＞0的解集为{x|-1＜x＜3}，求a，b的值．
7．已知定义域为[-6，6]的函数f（x），恒有f（x）+f（y）=f（x+y），且f（1）+f（-2）=$\frac{1}{2}$
（1）证明：f（x）+f（-x）=0，并求f（1），f（4）的值；
（2）如果x＞0时，f（x）＜0，解不等式f（x-1）＞-2．
17．甲、乙、丙、丁4个足球队举行单循环赛，列出：
（1）所有各场比赛的双方；
（2）所有冠亚军的可能情况（冠亚军不能并列）．
4．已知在数列{an}中，an＞0，2$\sqrt{{S}_{n}}$=an+1（n∈N+），求通项公式an．
8．已知函数f（x）=x-$\frac{a}{x}$-2lnx，a∈R．
（1）讨论函数f（x）的单调性；
（2）若函数f（x）有两个极值点x1，x2，且x1＜x2，
①求a的取值范围；
②证明：f（x2）＜x2-1．
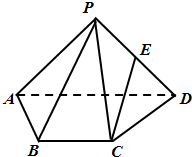9．如图，四棱锥P-ABCD中，PA⊥PD，AD⊥CD，PA=PD，AD∥BC，AB=AD=2BC=2，E是棱PD的中点，设二面角P-AD-B的值为θ．
（Ⅰ）当θ=$\frac{π}{2}$时，求证：AP⊥CE；
（Ⅱ）当θ=$\frac{π}{6}$时，求二面角P-AB-D的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网