题目内容
14.在棱长为1的正方体ABCD-A1B1C1D1中,A1C与平面ABCD所成的角为( )| A. | $\frac{π}{6}$ | B. | arctan$\frac{\sqrt{3}}{3}$ | C. | $\frac{π}{3}$ | D. | arctan$\frac{\sqrt{2}}{2}$ |
分析 由AA1⊥底面ABCD,得∠A1CA是A1C与平面ABCD所成的角,由此能求出A1C与平面ABCD所成的角的大小.
解答  解:∵AA1⊥底面ABCD,
解:∵AA1⊥底面ABCD,
∴∠A1CA是A1C与平面ABCD所成的角,
∵正方体ABCD-A1B1C1D1中棱长为1,
∴AC=$\sqrt{1+1}=\sqrt{2}$,${A}_{1}C=\sqrt{2+1}$=$\sqrt{3}$,
∴tan∠A1AC=$\frac{A{A}_{1}}{AC}$=$\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,
∴∠A1CA=arctan$\frac{\sqrt{2}}{2}$.
∴A1C与平面ABCD所成的角为arctan$\frac{\sqrt{2}}{2}$.
故选:D.
点评 本题考查线面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
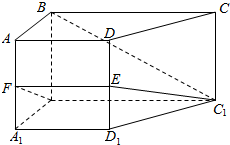 如图所示,在侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB═$\sqrt{2}$,AD=2,BC=4,AA1=2,E,F分别是DD1,AA1的中点.
如图所示,在侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB═$\sqrt{2}$,AD=2,BC=4,AA1=2,E,F分别是DD1,AA1的中点.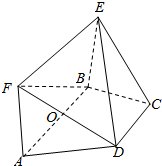 如图,几何体ABCDEF中,四边形ABEF为矩形,ABCD为梯形,平面ABEF⊥平面ABCD,AB∥CD,AB=4,AF=AD=CD=2,AD⊥BD,O为AB的中点.
如图,几何体ABCDEF中,四边形ABEF为矩形,ABCD为梯形,平面ABEF⊥平面ABCD,AB∥CD,AB=4,AF=AD=CD=2,AD⊥BD,O为AB的中点.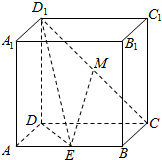 在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2,点E是线段AB的中点,点M为线段D1C上的动点.,
在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2,点E是线段AB的中点,点M为线段D1C上的动点.,