题目内容
已知α、β是三次函数f(x)=
x3+
ax2+2bx(a，b∈R)的两个极值点，且α∈（0，1），β∈（1，2），则
的取值范围是______．
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
f′（x）=x2+ax+2b
∵α，β是f（x）的极值点，
所以α，β是x2+ax+2b=0的两个根
∴α+β=-a，αβ=2b
∵α∈（0，1），β∈（1，2），
∴1＜α+β＜3，0＜αβ＜2
∴1＜-a＜3，0＜2b＜2
∴
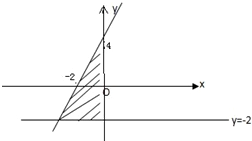
作出不等式组∴
的可行域
表示可行域中的点与（1，2）连线的斜率
有图知，当当点为（-3，1）和（-1，0）时分别为斜率的最小、最大值
所以此时两直线的斜率分别是
=
，
=1
故答案为(
，1)
∵α，β是f（x）的极值点，
所以α，β是x2+ax+2b=0的两个根
∴α+β=-a，αβ=2b
∵α∈（0，1），β∈（1，2），
∴1＜α+β＜3，0＜αβ＜2
∴1＜-a＜3，0＜2b＜2
∴
|
作出不等式组∴
|
| b-2 |
| a-1 |
有图知，当当点为（-3，1）和（-1，0）时分别为斜率的最小、最大值
所以此时两直线的斜率分别是
| 2-1 |
| 1--3 |
| 1 |
| 4 |
| 2-0 |
| 1-(-1) |
故答案为(
| 1 |
| 4 |
练习册系列答案
相关题目
