题目内容
某服装制造商现有10m2的棉布料,10m2的羊毛料,和6m2的丝绸料.做一条裤子需要1m2的棉布料,2m2的羊毛料,1m2的丝绸料.一条裙子需要1m2的棉布料,1m2的羊毛料,1m2的丝绸料.一条裤子的纯收益是50元,一条裙子的纯收益是40元,则该服装制造商的最大收益为______元.
设生产裤子x条,裙子y条,(x,y∈N),则根据条件建立不等式组
,作出不等式组对应的平面图象如图:
设收益为z,则目标函数z=50x+40y,
则y=-
x+
,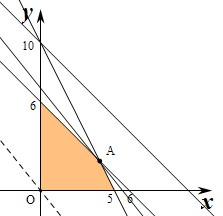
平移直线y=-
x+
,由图象可知当直线y=-
x+
经过点a时,直线y=-
x+
截距最大,此时z也最大,
由
,解得
,即A(4,2),
代入目标函数z=50x+40y得z=50×4+40×2=280(元).
故答案为:280.
|
设收益为z,则目标函数z=50x+40y,
则y=-
| 5 |
| 4 |
| z |
| 40 |

平移直线y=-
| 5 |
| 4 |
| z |
| 40 |
| 5 |
| 4 |
| z |
| 40 |
| 5 |
| 4 |
| z |
| 40 |
由
|
|
代入目标函数z=50x+40y得z=50×4+40×2=280(元).
故答案为:280.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目