题目内容
已知函数f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R),其中x∈[0,15],a>0,且a≠1.
(1)若1是关于x的方程f(x)-g(x)=0的一个解,求t的值;
(2)当0<a<1时,不等式f(x)≥g(x)恒成立,求t的取值范围;
(3)当t∈[26,56]时,函数F(x)=2g(x)-f(x)的最小值为h(t),求h(t)的解析式.
解:(1)由题意得f(1)-g(1)=0,即loga2=2loga(2+t),解得t=-2+ …(2分)
…(2分)
(2)当0<a<1时,不等式f(x)≥g(x)恒成立,即 loga(x+1)≥loga(2x+t)(x∈[0,15])恒成立,
loga(x+1)≥loga(2x+t)(x∈[0,15])恒成立,
它等价于 ≤2x+t(x∈[0,15]),即t≥
≤2x+t(x∈[0,15]),即t≥ -2x(x∈[0,15])恒成立…(6分)
-2x(x∈[0,15])恒成立…(6分)
令 =u(x∈[0,15]),则u∈[1,4],x=u2-1,
=u(x∈[0,15]),则u∈[1,4],x=u2-1,
 -2x=-2(u2-1)+u=-2
-2x=-2(u2-1)+u=-2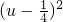 +
+ ,当u=1时,
,当u=1时, -2x的最大值为1,
-2x的最大值为1,
∴t≥1…(8分)
(3)F(x)=2g(x)-f(x)=4loga(2x+t)-loga(x+1)=4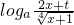 .
.
令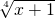 =z (x∈[0,15]),则z∈[1,2],x=z4-1,
=z (x∈[0,15]),则z∈[1,2],x=z4-1,
∴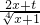 =
=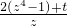 =2z3+
=2z3+ ,z∈[1,2],…(10分)
,z∈[1,2],…(10分)
设p(z)=2z3+ ,z∈[1,2],
,z∈[1,2],
则p′(z)=6z2-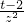 .
.
令p'(z)=0,得z=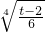 .
.
∵t∈[26,56],
∴z=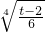 ∈[
∈[ ,
, ]⊆[1,2],
]⊆[1,2],
当1≤z≤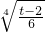 时,p'(z)<0;
时,p'(z)<0;
当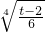 <z≤2,p'(z)>0.
<z≤2,p'(z)>0.
故[p(z)]min= =8
=8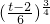 ,…(12分)
,…(12分)
且p(z)的最大值只能在z=1或z=2处取得.
而p(1)=2+t-2=t,p(2)=16+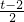 =
= +15,
+15,
∴p(1)-p(2)= -15,
-15,
当26≤t≤30时,p(1)≤p(2),p(z)max=p(2)= +15,
+15,
当30<t≤56时,p(1)>p(2),p(z)max=p(1)=t,
∴p(z)max=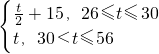 …(14分)
…(14分)
∴当a>1时,h(t)=4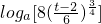 ;
;
当0<a<1时,h(t)=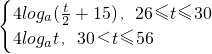 …(16分)
…(16分)
分析:(1)由f(1)-g(1)=0,即可求得t的值;
(2)当0<a<1时,不等式f(x)≥g(x)恒成立?t≥ -2x(x∈[0,15])恒成立,令
-2x(x∈[0,15])恒成立,令 =u(x∈[0,15]),则u∈[1,4],通过配方法可求得
=u(x∈[0,15]),则u∈[1,4],通过配方法可求得 -2x的最大值,从而解决问题;
-2x的最大值,从而解决问题;
(3)F(x)=2g(x)-f(x)=4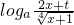 ,令
,令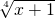 =z 可求得z∈[1,2],设p(z)=2z3+
=z 可求得z∈[1,2],设p(z)=2z3+ ,z∈[1,2],通过导数可求得[p(z)]min与[p(z)]max,从而可得答案.
,z∈[1,2],通过导数可求得[p(z)]min与[p(z)]max,从而可得答案.
点评:本题考查函数恒成立问题,考查对数函数图象与性质的综合应用,考查等价转化的思想与分类讨论的思想,考查换元的方法与导数法的应用,综合性强,难度大,属于难题.
 …(2分)
…(2分)(2)当0<a<1时,不等式f(x)≥g(x)恒成立,即
 loga(x+1)≥loga(2x+t)(x∈[0,15])恒成立,
loga(x+1)≥loga(2x+t)(x∈[0,15])恒成立,它等价于
 ≤2x+t(x∈[0,15]),即t≥
≤2x+t(x∈[0,15]),即t≥ -2x(x∈[0,15])恒成立…(6分)
-2x(x∈[0,15])恒成立…(6分)令
 =u(x∈[0,15]),则u∈[1,4],x=u2-1,
=u(x∈[0,15]),则u∈[1,4],x=u2-1, -2x=-2(u2-1)+u=-2
-2x=-2(u2-1)+u=-2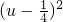 +
+ ,当u=1时,
,当u=1时, -2x的最大值为1,
-2x的最大值为1,∴t≥1…(8分)
(3)F(x)=2g(x)-f(x)=4loga(2x+t)-loga(x+1)=4
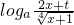 .
.令
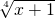 =z (x∈[0,15]),则z∈[1,2],x=z4-1,
=z (x∈[0,15]),则z∈[1,2],x=z4-1,∴
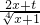 =
=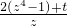 =2z3+
=2z3+ ,z∈[1,2],…(10分)
,z∈[1,2],…(10分)设p(z)=2z3+
 ,z∈[1,2],
,z∈[1,2],则p′(z)=6z2-
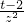 .
.令p'(z)=0,得z=
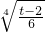 .
.∵t∈[26,56],
∴z=
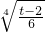 ∈[
∈[ ,
, ]⊆[1,2],
]⊆[1,2],当1≤z≤
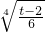 时,p'(z)<0;
时,p'(z)<0;当
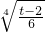 <z≤2,p'(z)>0.
<z≤2,p'(z)>0.故[p(z)]min=
 =8
=8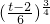 ,…(12分)
,…(12分)且p(z)的最大值只能在z=1或z=2处取得.
而p(1)=2+t-2=t,p(2)=16+
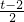 =
= +15,
+15,∴p(1)-p(2)=
 -15,
-15,当26≤t≤30时,p(1)≤p(2),p(z)max=p(2)=
 +15,
+15,当30<t≤56时,p(1)>p(2),p(z)max=p(1)=t,
∴p(z)max=
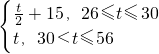 …(14分)
…(14分)∴当a>1时,h(t)=4
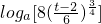 ;
;当0<a<1时,h(t)=
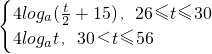 …(16分)
…(16分)分析:(1)由f(1)-g(1)=0,即可求得t的值;
(2)当0<a<1时,不等式f(x)≥g(x)恒成立?t≥
 -2x(x∈[0,15])恒成立,令
-2x(x∈[0,15])恒成立,令 =u(x∈[0,15]),则u∈[1,4],通过配方法可求得
=u(x∈[0,15]),则u∈[1,4],通过配方法可求得 -2x的最大值,从而解决问题;
-2x的最大值,从而解决问题;(3)F(x)=2g(x)-f(x)=4
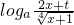 ,令
,令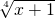 =z 可求得z∈[1,2],设p(z)=2z3+
=z 可求得z∈[1,2],设p(z)=2z3+ ,z∈[1,2],通过导数可求得[p(z)]min与[p(z)]max,从而可得答案.
,z∈[1,2],通过导数可求得[p(z)]min与[p(z)]max,从而可得答案.点评:本题考查函数恒成立问题,考查对数函数图象与性质的综合应用,考查等价转化的思想与分类讨论的思想,考查换元的方法与导数法的应用,综合性强,难度大,属于难题.

练习册系列答案
相关题目