题目内容
9.在与水平地面垂直的墙壁上挂有一幅矩形画,画的上下边缘在观察着水平视线上方a m和b m处,要使观察者的视角最大,观察者与墙的距离为( )| A. | $\sqrt{ab}m$ | B. | $\frac{a+b}{2}m$ | C. | am | D. | bm |
分析 作出图象,由题意可得OA=b,OB=a,设OM=x,∠OMA=α,∠OMB=β,由三角函数的定义可得tanα=$\frac{b}{x}$,tanβ=$\frac{a}{x}$,再由两角差的正切公式可得tan(β-α)=$\frac{tanβ-tanα}{1+tanβtanα}$=$\frac{\frac{a}{x}-\frac{b}{x}}{1+\frac{ab}{{x}^{2}}}$=$\frac{a-b}{x+\frac{ab}{x}}$,由基本不等式可得.
解答 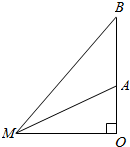 解:如图所示观察者在M处,A、B为画的下、上边缘,
解:如图所示观察者在M处,A、B为画的下、上边缘,
由题意可得OA=b,OB=a,设OM=x,∠OMA=α,∠OMB=β,
则分别在直角三角形中可得tanα=$\frac{b}{x}$,tanβ=$\frac{a}{x}$,
∴tan(β-α)=$\frac{tanβ-tanα}{1+tanβtanα}$
=$\frac{\frac{a}{x}-\frac{b}{x}}{1+\frac{ab}{{x}^{2}}}$=$\frac{a-b}{x+\frac{ab}{x}}$≤$\frac{a-b}{2\sqrt{ab}}$
当且仅当x=$\frac{ab}{x}$即x=$\sqrt{ab}$时取等号,
由∵y=tanx在(0,$\frac{π}{2}$)为增函数,
∴当x=$\sqrt{ab}$时,视角最大.
故选:A.
点评 本题考查基本不等式求最值的实际应用,涉及正切函数的单调性和两角差的正切公式,属中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
19.数据5,7,7,8,10,11的方差是( )
| A. | 24 | B. | 10 | C. | 4 | D. | 2 |
20.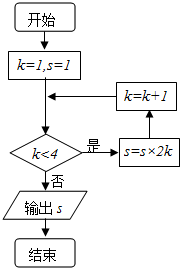 执行如图所示的程序框图,输出的s值为( )
执行如图所示的程序框图,输出的s值为( )
 执行如图所示的程序框图,输出的s值为( )
执行如图所示的程序框图,输出的s值为( )| A. | 8 | B. | 16 | C. | 48 | D. | 64 |