题目内容
(12分)已知函数f(X)=sin2X+acos2X (a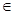 R) 且
R) 且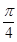 是函数Y=f(X)的零点
是函数Y=f(X)的零点
(1)求a的值,并求函数f(X)的最小正周期
(2)若X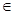 〔0,
〔0, 〕,求函数f(X)的值域
〕,求函数f(X)的值域
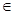 R) 且
R) 且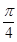 是函数Y=f(X)的零点
是函数Y=f(X)的零点(1)求a的值,并求函数f(X)的最小正周期
(2)若X
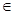 〔0,
〔0, 〕,求函数f(X)的值域
〕,求函数f(X)的值域解:(1)由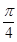 是函数Y=f(X)的零点得f(
是函数Y=f(X)的零点得f(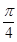 )=0 即sin
)=0 即sin +acos2
+acos2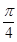 =0 得a=-2
=0 得a=-2
∴f(X)=sin2X-2cos2X=sin2X-cos2X-1=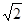 sin(2X-
sin(2X-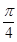 )-1 ∴T=
)-1 ∴T=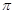
(2) ∵X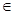 〔0,
〔0, 〕 ∴2X-
〕 ∴2X-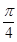
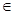 〔-
〔-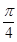 ,
,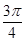 〕则sin(2X-
〕则sin(2X-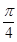 )
)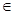 〔-
〔-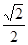 ,1〕
,1〕
∴-2≤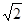 sin(2X-
sin(2X-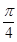 )-1≤
)-1≤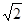 -1 ∴值域为〔-2,
-1 ∴值域为〔-2,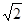 -1〕
-1〕
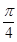 是函数Y=f(X)的零点得f(
是函数Y=f(X)的零点得f(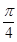 )=0 即sin
)=0 即sin +acos2
+acos2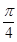 =0 得a=-2
=0 得a=-2∴f(X)=sin2X-2cos2X=sin2X-cos2X-1=
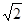 sin(2X-
sin(2X-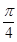 )-1 ∴T=
)-1 ∴T=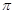
(2) ∵X
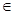 〔0,
〔0, 〕 ∴2X-
〕 ∴2X-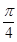
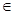 〔-
〔-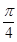 ,
,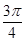 〕则sin(2X-
〕则sin(2X-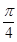 )
)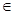 〔-
〔-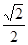 ,1〕
,1〕∴-2≤
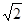 sin(2X-
sin(2X-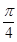 )-1≤
)-1≤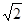 -1 ∴值域为〔-2,
-1 ∴值域为〔-2,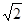 -1〕
-1〕略

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
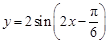 的图象( )
的图象( ) 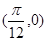 成中心对称
成中心对称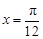 成轴对称
成轴对称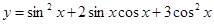 ,
,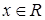 ,那么
,那么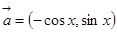 ,
,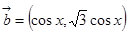 ,函数
,函数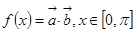 .
. 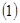 求函数
求函数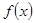 的最大值;
的最大值;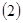 当函数
当函数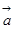 与
与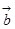 夹角的大小。
夹角的大小。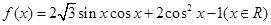
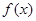 的最小正周期及在区间
的最小正周期及在区间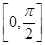
 上的最大值和最小值;
上的最大值和最小值;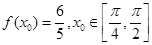 ,求
,求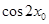 的值。
的值。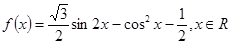 .
.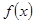 的最大值,并求使
的最大值,并求使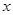 的集合
的集合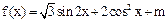 在区间[
在区间[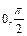 ]上的最大值为6,
]上的最大值为6,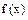 关于y轴的对称图象得函数
关于y轴的对称图象得函数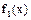 的图象,再把
的图象,再把 个单位得
个单位得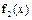 的图象,求函数
的图象,求函数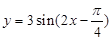 的图像,只需将函数
的图像,只需将函数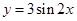 的图像向 平移 个单位.
的图像向 平移 个单位.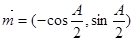 ,
, 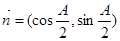 , 且
, 且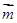 ·
·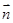 =
=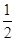 .
.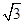 ,三角形面积S=
,三角形面积S=