题目内容
【题目】已知点M是圆C:(x+1)2+y2=8上的动点,定点D(1,0),点P在直线DM上,点N在直线CM上,且满足![]() 2
2![]() ,
,![]()
![]() 0,动点N的轨迹为曲线E.
0,动点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若AB是曲线E的长为2的动弦,O为坐标原点,求△AOB面积S的最大值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)由已知得NP为DM的垂直平分线,|ND|=|NM|,![]() ,由此能求了轨迹E的方程.
,由此能求了轨迹E的方程.
(2)法一:设直线AB的方程为y=kx+m,由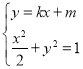 ,得(1+2k2)x2+4kmx+2m2﹣2=0.由此利用根的判别式、韦达定理、弦长公式、点到直线的距离公式,结合已知条件能求出△AOB面积S的最大值.
,得(1+2k2)x2+4kmx+2m2﹣2=0.由此利用根的判别式、韦达定理、弦长公式、点到直线的距离公式,结合已知条件能求出△AOB面积S的最大值.
(2)法二:设直线AB的方程为y=kx+m,由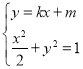 ,得(1+2k2)x2+4kmx+2m2﹣2=0.由此利用根的判别式、韦达定理、点到直线的距离公式,结合已知条件能求出△AOB面积S的最大值.
,得(1+2k2)x2+4kmx+2m2﹣2=0.由此利用根的判别式、韦达定理、点到直线的距离公式,结合已知条件能求出△AOB面积S的最大值.
(1)解:因为![]() ,
,![]() ,
,
所以NP为DM的垂直平分线,
所以|ND|=|NM|,又因为![]() ,
,
所以![]()
所以动点N的轨迹是以点C(﹣1,0),D(1,0)为焦点的长轴为![]() 的椭圆.
的椭圆.
所以轨迹E的方程为![]() .
.
(2)解法一:因为线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,
则弦AB不能与x轴垂直,故可设直线AB的方程为y=kx+m,
由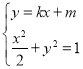 ,消去y,并整理,得(1+2k2)x2+4kmx+2m2﹣2=0.
,消去y,并整理,得(1+2k2)x2+4kmx+2m2﹣2=0.
设A(x1,y1),B(x2,y2),又△=16k2m2﹣4(1+2k2)(2m2﹣2)>0,
所以![]() ,
,![]()
因为|AB|=2,所以![]() ,即
,即![]()
所以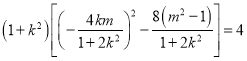 ,即
,即![]() ,
,
因为1+k2≥1,所以![]() .
.
又点O到直线AB的距离![]() ,
,
因为![]() h,
h,
所以S2=h2=2m2(1﹣m2)![]()
所以![]() ,即S的最大值为
,即S的最大值为![]() .
.
(2)解法二:因为线段AB的长等于椭圆短轴的长,要使三点A、O、B能构成三角形,
则弦AB不能与x垂直,故可设直线AB的方程为y=kx+m,
由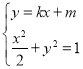 ,消去y,并整理,得(1+2k2)x2+4kmx+2m2﹣2=0.
,消去y,并整理,得(1+2k2)x2+4kmx+2m2﹣2=0.
设A(x1,y1),B(x2,y2),又△=16k2m2﹣4(1+2k2)(2m2﹣2)>0,
所以![]() ,
,![]() .
.
因为|AB|=2,所以![]() .
.
因为![]() ,
,
所以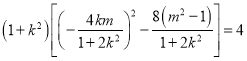 ,
,
所以 ,
,
又点O到直线AB的距离![]() ,所以
,所以![]() h.
h.
所以S2=h2 .
.
设![]() ,则
,则![]() ,
,
所以![]() ,即S的最大值为
,即S的最大值为![]() .
.