题目内容
已知各项均不为零的数列{an},定义向量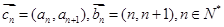 .下列命题中真命题是
.下列命题中真命题是
A.若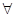 n∈N*总有 n∈N*总有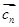 ∥ ∥ 成立,则数列{an}是等差数列; 成立,则数列{an}是等差数列; |
B.若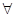 n∈N*总有 n∈N*总有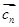 ∥ ∥ 成立,则数列{an}是等比数列; 成立,则数列{an}是等比数列; |
C.若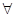 n∈N*总有 n∈N*总有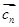 ⊥ ⊥ 成立,则数列{an}是等差数列; 成立,则数列{an}是等差数列; |
D.若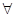 n∈N*总有 n∈N*总有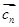 ⊥ ⊥ 成立,则数列{an}是等比数列. 成立,则数列{an}是等比数列. |
A
解析试题分析:因为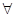 n∈N*总有
n∈N*总有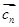 ∥
∥ 成立,所以
成立,所以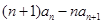 =0,
=0,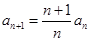 ;
;
从而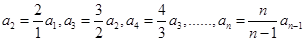 ,所以
,所以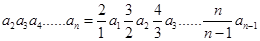 ,
,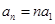 ,即数列{an}是等差数列,故选A。
,即数列{an}是等差数列,故选A。
考点:本题主要考查递推数列、命题及复合命题的概念,向量的坐标运算。
点评:简单题,准确计算向量的数量积是基础,利用“累乘法”是关键。

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知等差数列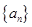 满足
满足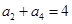 ,
, 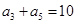 ,则它的前10项和
,则它的前10项和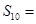 ( )
( )
| A.85 | B.135 | C.95 | D.23 |
设数列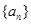 的前n项和为
的前n项和为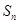 ,令
,令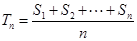 ,称
,称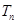 为数列
为数列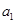 ,
,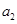 , ,
, ,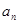 的“理想数”,已知数列
的“理想数”,已知数列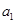 ,
,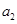 , ,
, ,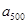 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 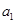 ,
,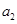 , ,
, ,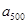 的“理想数”为
的“理想数”为
| A.2008 | B.2004 | C.2002 | D.2000 |
已知数列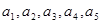 的各项均不等于0和1,此数列前
的各项均不等于0和1,此数列前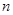 项的和为
项的和为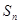 ,且满足
,且满足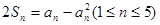 ,则满足条件的数列共有( )
,则满足条件的数列共有( )
| A. 2个 | B. 6个 | C. 8个 | D. 16个 |
数列 满足
满足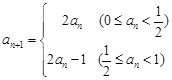 ,若
,若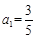 ,则
,则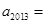 ( )
( )
A.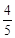 | B.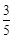 | C.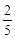 | D.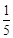 |
定义:数列 ,满足
,满足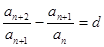
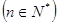 d为常数,我们称
d为常数,我们称 为等差比数列,已知在等差比数列
为等差比数列,已知在等差比数列 中,
中,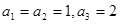 ,则
,则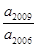 的个位数( )
的个位数( )
| A.3 | B.4 | C.6 | D.8 |
在数列 中,
中, 则
则 的值为 ( )
的值为 ( )
| A.49 | B. 50 | C.51 | D.52 |
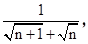 已知它的前n项和Sn=6,则项数n等于 .
已知它的前n项和Sn=6,则项数n等于 . ,若{an}的前n项和为24,则n为________.
,若{an}的前n项和为24,则n为________.