题目内容
椭圆与直线x+y=1交于A,B两点,点C是线段AB的中点,且|AB|=2
,直线OC的斜率为
,求椭圆的标准方程.
| 2 |
| ||
| 2 |
分析:设椭圆的方程为mx2+ny2=1,将椭圆方程与直线x+y=1联解消去y得到关于x的一元二次方程,利用根与系数的关系与弦长公式,结合题意建立m、n的关系式,化简得m-mn+n=(m+n)2.再由点C是线段AB的中点,利用中点坐标公式和斜率公式,列式并化简得到
=
,联解得到m、n的值,即可得到所求椭圆的标准方程.
| m |
| n |
| ||
| 2 |
解答:解:根据题意,设椭圆的方程是:mx2+ny2=1,(m、n为不相等的正数).
由
,消去y得:(m+n)x2-2nx+n-1=0;
设A(x1,y1),B(x2,y2),可得x1+x2=
,x1x2=
,
∴|x1-x2|=
=
∵|AB|=2
,直线OC的斜率k=
,
∴|AB|=
|x1-x2|=
=2
,
化简得m-mn+n=(m+n)2…①,
∵点C是线段AB的中点,
∴设C(λ,μ),可得λ =
(x1+x2)=
,μ =1-xC=
因此,OC的斜率kOC=
=
=
…②
联解①②,可得m=
,n=
,
∴所求椭圆标准方程为
x2+
y2=1,化简得
+
=1.
由
|
设A(x1,y1),B(x2,y2),可得x1+x2=
| 2n |
| m+n |
| n-1 |
| m+n |
∴|x1-x2|=
| (x1+x2)2-4x 1x2 |
| ||
| m+n |
∵|AB|=2
| 2 |
| ||
| 2 |
∴|AB|=
| 1+k2 |
2
| ||||
| m+n |
| 2 |
化简得m-mn+n=(m+n)2…①,
∵点C是线段AB的中点,
∴设C(λ,μ),可得λ =
| 1 |
| 2 |
| n |
| m+n |
| m |
| m+n |
因此,OC的斜率kOC=
| μ |
| λ |
| m |
| n |
| ||
| 2 |
联解①②,可得m=
| 1 |
| 3 |
| ||
| 3 |
∴所求椭圆标准方程为
| 1 |
| 3 |
| ||
| 3 |
| x2 |
| 3 |
| y2 | ||||
|
点评:本题着重考查了椭圆的标准方程、直线的斜率公式、一元二次方程根与系数的关系和直线与椭圆的位置关系等知识,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 与直线x+y-1=0相交于P、Q两点,且
与直线x+y-1=0相交于P、Q两点,且 (O为坐标原点).
(O为坐标原点). 等于定值;
等于定值;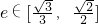 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围. 与直线x+y-1=0相交于P、Q两点,且OP⊥OQ(O为原点),
与直线x+y-1=0相交于P、Q两点,且OP⊥OQ(O为原点),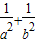 的值;
的值;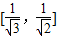 上变化时,求椭圆长轴的取值范围.
上变化时,求椭圆长轴的取值范围.