题目内容
椭圆 与直线x+y-1=0相交于P、Q两点,且
与直线x+y-1=0相交于P、Q两点,且 (O为坐标原点).
(O为坐标原点).
(Ⅰ)求证: 等于定值;
等于定值;
(Ⅱ)当椭圆的离心率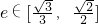 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围.
(1)证明: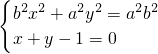
消去y得(a2+b2)x2-2a2x+a2(1-b2)=0
△=4a4-4(a2+b2)a2(1-b2)>0,a2+b2>1
设点P(x1,y1),Q(x2,y2),
则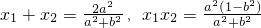 ,
,
由 ,x1x2+y1y2=0,
,x1x2+y1y2=0,
即x1x2+(1-x1)(1-x2)=0
化简得2x1x2-(x1+x2)+1=0,
则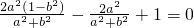
即a2+b2=2a2b2,故
(Ⅱ)解:由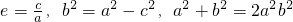
化简得
由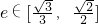 得
得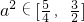 ,
,
即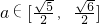
故椭圆的长轴长的取值范围是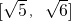 .
.
分析:(Ⅰ)联立方程组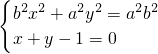 ,消去y得(a2+b2)x2-2a2x+a2(1-b2)=0,由△>0推出a2+b2>1,设点P(x1,y1),Q(x2,y2),由
,消去y得(a2+b2)x2-2a2x+a2(1-b2)=0,由△>0推出a2+b2>1,设点P(x1,y1),Q(x2,y2),由 ,得x1x2+y1y2=0,由此能够推导出
,得x1x2+y1y2=0,由此能够推导出 .
.
(Ⅱ)由由、题高级条件能够推导出 ,再由
,再由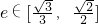 得
得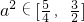 ,由此能够推陈出新导出长轴长的取值范围.
,由此能够推陈出新导出长轴长的取值范围.
点评:本题考查椭圆的性质和应用,具有一定的难度,解题时要细心解答,避免出现不必要的错误.
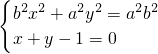
消去y得(a2+b2)x2-2a2x+a2(1-b2)=0
△=4a4-4(a2+b2)a2(1-b2)>0,a2+b2>1
设点P(x1,y1),Q(x2,y2),
则
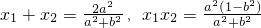 ,
,由
 ,x1x2+y1y2=0,
,x1x2+y1y2=0,即x1x2+(1-x1)(1-x2)=0
化简得2x1x2-(x1+x2)+1=0,
则
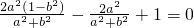
即a2+b2=2a2b2,故

(Ⅱ)解:由
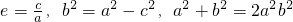
化简得

由
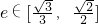 得
得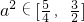 ,
,即
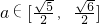
故椭圆的长轴长的取值范围是
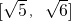 .
.分析:(Ⅰ)联立方程组
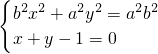 ,消去y得(a2+b2)x2-2a2x+a2(1-b2)=0,由△>0推出a2+b2>1,设点P(x1,y1),Q(x2,y2),由
,消去y得(a2+b2)x2-2a2x+a2(1-b2)=0,由△>0推出a2+b2>1,设点P(x1,y1),Q(x2,y2),由 ,得x1x2+y1y2=0,由此能够推导出
,得x1x2+y1y2=0,由此能够推导出 .
.(Ⅱ)由由、题高级条件能够推导出
 ,再由
,再由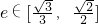 得
得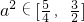 ,由此能够推陈出新导出长轴长的取值范围.
,由此能够推陈出新导出长轴长的取值范围.点评:本题考查椭圆的性质和应用,具有一定的难度,解题时要细心解答,避免出现不必要的错误.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 与直线x+y-1=0相交于P、Q两点,且OP⊥OQ(O为原点),
与直线x+y-1=0相交于P、Q两点,且OP⊥OQ(O为原点),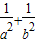 的值;
的值;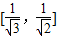 上变化时,求椭圆长轴的取值范围.
上变化时,求椭圆长轴的取值范围.