题目内容
已知复数z满足z=(-1+3i)(1-i)-4.(1)求复数z的共轭复数
 ;
;(2)若w=z+ai,且|w|≤|z|,求实数a的取值范围.
【答案】分析:(1)利用i2=-1对z进行化简,并整理出实部和虚部,再由由共轭复数的定义求出;
(2)根据(1)求出的结果和复数模的公式求出|z|,再结合条件表示出|w|,根据题意列出关于a的不等式,利用二次不等式的解法求出a的范围.
解答:解:(1)∵z=(-1+3i)(1-i)-4=-1+i+3i+3-4=-2+4i,
∴
(2)由(1)知z=-2+4i,∴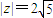 ,
,
∵w=-2+(4+a)i,∴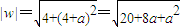
∵|w|≤|z|,∴20+8a+a2≤20,∴a2+8a≤0,∴a(a+8)≤0,
∴实数a的取值范围是:-8≤a≤0.
点评:本题是有关复数的综合题,考查了共轭复数的定义,复数模的公式的应用,以及二次不等式的解法.
(2)根据(1)求出的结果和复数模的公式求出|z|,再结合条件表示出|w|,根据题意列出关于a的不等式,利用二次不等式的解法求出a的范围.
解答:解:(1)∵z=(-1+3i)(1-i)-4=-1+i+3i+3-4=-2+4i,
∴

(2)由(1)知z=-2+4i,∴
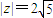 ,
,∵w=-2+(4+a)i,∴
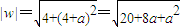
∵|w|≤|z|,∴20+8a+a2≤20,∴a2+8a≤0,∴a(a+8)≤0,
∴实数a的取值范围是:-8≤a≤0.
点评:本题是有关复数的综合题,考查了共轭复数的定义,复数模的公式的应用,以及二次不等式的解法.

练习册系列答案
相关题目