题目内容
A(1,3),B(5,-2),点P在x轴上使|AP|-|BP|最大,则P的坐标为( )A.(4,0)
B.(13,0)
C.(5,0)
D.(1,0)
【答案】分析:求出B关于x轴的对称点C,然后求出AC的直线方程,然后求出直线与x轴的交点,就是P的坐标.
解答:解:点B关于x轴的对称点为C,C(5,2),
所以直线AC的方程为:y-3=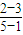 (x-1)=-
(x-1)=-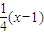 .即4y+x-13=0.
.即4y+x-13=0.
令y=0,可得x=13,
所以P(13,0).
故选B.
点评:本题考查点关于直线对称点的求法,考查分析问题与解答问题的能力.
解答:解:点B关于x轴的对称点为C,C(5,2),
所以直线AC的方程为:y-3=
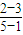 (x-1)=-
(x-1)=-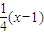 .即4y+x-13=0.
.即4y+x-13=0.令y=0,可得x=13,
所以P(13,0).
故选B.
点评:本题考查点关于直线对称点的求法,考查分析问题与解答问题的能力.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
以A(1,3)和B(-5,1)为端点的线段AB的中垂线方程是( )
| A、3x-y+8=0 | B、3x+y+4=0 | C、2x-y-6=0 | D、3x+y+8=0 |
已知三点A(1,3)、B(5,7)、C(10,12).则下列说法中正确的是( )
| A、A、B、C三点共线 | B、△ABC是Rt△ | C、A、B、C三点不共线 | D、△ABC是等边三角形 |