题目内容
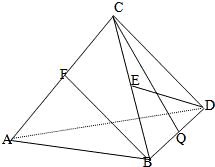
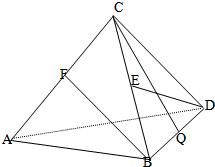 四面体C-ABD中,CB=CD,AB=AD,∠BAD=90°. E、F,Q分别是BC、AC、BD的中点.
四面体C-ABD中,CB=CD,AB=AD,∠BAD=90°. E、F,Q分别是BC、AC、BD的中点.(1)求证:AC⊥BD;
(2)在AC上确定一点M,使BF∥平面MED?并说明理由;
(3)若CQ为底面ABD的一条斜线段,请问CA,CB有可能相等吗?证明你的结论.
分析:(1)考虑到CB=CD,AB=AD,Q是BD的中点,故连接CQ、AQ,从而可得AQ⊥BD,CQ⊥BD,根据线面垂直的判定定理可证.
(2)由于F,E分别为AC,BC的中点,故考虑取FC的中点,从而有ME∥BQ,根据线与平面平行的判定定理可得
(3)假设CA=CB,则CA=CB=CD,则C在平面ABD的射影O为三角形ABD的外心,结合已知可得O与Q重合,即CQ⊥平面ABD,与已知矛盾,故不可能有CA=CB
(2)由于F,E分别为AC,BC的中点,故考虑取FC的中点,从而有ME∥BQ,根据线与平面平行的判定定理可得
(3)假设CA=CB,则CA=CB=CD,则C在平面ABD的射影O为三角形ABD的外心,结合已知可得O与Q重合,即CQ⊥平面ABD,与已知矛盾,故不可能有CA=CB
解答:解:(1)连接CQ,AQ∵CB=CD,AB=AD且Q是BD的中点
∴BD⊥AQBD⊥CQ∵CQ∩AQ=Q
∴BD⊥平面AQC,∴BD⊥AC
(II)当M为CF的中点,即CM=
CA时,可得BF∥EM
∵BF?平面MED,ME⊆平面MED
∴BF∥平面MED
(3)假设CA=CB,则CA=CB=CD,过C作CO⊥平面ABD,则O为△ABD的外心,即OA=OB=OD,
又△ABD为直角三角形,∠BAD=90°,
∴O为BD的中点从而O与Q重合
∴CQ⊥平面ABD 与CQ为底面ABD的一条斜线段矛盾
故CA,CB不可能相等
∴BD⊥AQBD⊥CQ∵CQ∩AQ=Q
∴BD⊥平面AQC,∴BD⊥AC
(II)当M为CF的中点,即CM=
| 1 |
| 4 |
∵BF?平面MED,ME⊆平面MED
∴BF∥平面MED
(3)假设CA=CB,则CA=CB=CD,过C作CO⊥平面ABD,则O为△ABD的外心,即OA=OB=OD,
又△ABD为直角三角形,∠BAD=90°,
∴O为BD的中点从而O与Q重合
∴CQ⊥平面ABD 与CQ为底面ABD的一条斜线段矛盾
故CA,CB不可能相等
点评:本题主要考查了线与平面垂直与线与线垂直的相互转化,线与平面的平行的判定及“线线平行”与“线面平行”的转化,考查了空间想象能力及推理论证的能力.

练习册系列答案
相关题目

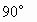 ,AC=BC,△ABD中,∠ABD=
,AC=BC,△ABD中,∠ABD=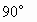 ,∠D=
,∠D=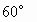 .设AC=a.现将四边形ACBD沿着AB翻折成直二面角C-AB-D,连结CD得一个四面体(如下图).
.设AC=a.现将四边形ACBD沿着AB翻折成直二面角C-AB-D,连结CD得一个四面体(如下图).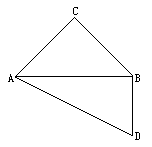
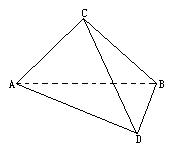
 四面体C-ABD中,CB=CD,AB=AD,∠BAD=90°. E、F,Q分别是BC、AC、BD的中点.
四面体C-ABD中,CB=CD,AB=AD,∠BAD=90°. E、F,Q分别是BC、AC、BD的中点.