题目内容
设双曲线C1的方程为
-
=1(a>0,b>0),A、B为其左、右两个顶点,P是双曲线C1上的任意一点,作QB⊥PB,QA⊥PA,垂足分别为A、B,AQ与BQ交于点Q.
(1)求Q点的轨迹C2方程;
(2)设C1、C2的离心率分别为e1、e2,当e1≥
时,求e2的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求Q点的轨迹C2方程;
(2)设C1、C2的离心率分别为e1、e2,当e1≥
| 2 |
分析:(1)欲求Q点的轨迹C2方程,设Q(x,y),即求出Q点的坐标之间的关系式,再设P(x0,y0),A(-a,0),B(a,0),利用QB⊥PB,QA⊥PA,直线的斜率之积为-1,即可建立Q点的坐标之间的关系式,从而得出Q点的轨迹C2方程;
(2)由(1)得C2的方程为
-
=1,利用其几何性质求出离心率,得出与e1的关系式,最后根据e1的范围即可得出e2的取值范围.
(2)由(1)得C2的方程为
| x2 |
| a2 |
| y2 | ||
|
解答: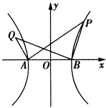 解:(1)如图,设P(x0,y0),Q(x,y),A(-a,0),B(a,0),QB⊥PB,QA⊥PA,
解:(1)如图,设P(x0,y0),Q(x,y),A(-a,0),B(a,0),QB⊥PB,QA⊥PA,
∴
两式相乘得:
•
=1①
∵
-
=1,∴
=
,代入①得b2y2=x2a2-a4,即a2x2-b2y2=a4.
经检验,点(-a,0),(a,0)不合题意,因此Q点的轨迹方程是a2x2-b2y2=a4(点(-a,0),(a,0)除外).
(2)由(1)得C2的方程为
-
=1.
=
=1+
=1+
=1+
,
∵e1≥
,∴e
≤1+
=2,
∴1<e≤
.
 解:(1)如图,设P(x0,y0),Q(x,y),A(-a,0),B(a,0),QB⊥PB,QA⊥PA,
解:(1)如图,设P(x0,y0),Q(x,y),A(-a,0),B(a,0),QB⊥PB,QA⊥PA,∴
|
两式相乘得:
| ||
|
| y2 |
| x2-a2 |
∵
| ||
| a2 |
| ||
| b2 |
| ||
|
| b2 |
| a2 |
经检验,点(-a,0),(a,0)不合题意,因此Q点的轨迹方程是a2x2-b2y2=a4(点(-a,0),(a,0)除外).
(2)由(1)得C2的方程为
| x2 |
| a2 |
| y2 | ||
|
| e | 2 2 |
a2+
| ||
| a2 |
| a2 |
| b2 |
| a2 |
| c2-a2 |
| 1 | ||
|
∵e1≥
| 2 |
2 2 |
| 1 | ||
(
|
∴1<e≤
| 2 |
点评:本小题主要考查双曲线的简单性质、直线垂直的条件、不等式、点的轨迹方程等基本知识,考查化归以及数形结合等数学思想方法,考查分析问题、解决问题的能力.

练习册系列答案
相关题目

 (a>0,b>0),A、B为其左、右两个顶点,P是双曲线C1上的任意一点,作QB⊥PB,QA⊥PA,垂足分别为A、B,AQ与BQ交于点Q.
(a>0,b>0),A、B为其左、右两个顶点,P是双曲线C1上的任意一点,作QB⊥PB,QA⊥PA,垂足分别为A、B,AQ与BQ交于点Q.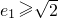 时,求e2的取值范围.
时,求e2的取值范围. (a>0,b>0),A、B为其左、右两个顶点,P是双曲线C1上的任意一点,作QB⊥PB,QA⊥PA,垂足分别为A、B,AQ与BQ交于点Q.
(a>0,b>0),A、B为其左、右两个顶点,P是双曲线C1上的任意一点,作QB⊥PB,QA⊥PA,垂足分别为A、B,AQ与BQ交于点Q.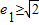 时,求e2的取值范围.
时,求e2的取值范围.