题目内容
设双曲线C1的方程为![]() ,A、B为其左、右两个顶点,P是双曲线C1上的任意一点,引QB⊥PB,QA⊥PA,AQ与BQ交于点Q.
,A、B为其左、右两个顶点,P是双曲线C1上的任意一点,引QB⊥PB,QA⊥PA,AQ与BQ交于点Q.
(1)求Q点的轨迹方程;
(2)设(I)中所求轨迹为C2,C1、C2
的离心率分别为e1、e2,当![]() 时,e2的取值范围.
时,e2的取值范围.

答案:
解析:
解析:
|
答案:a2x2-b2y2=a4(除点(-a,0),(a,0)外); (1)解法一:设P(x0,y0),Q(x ,y )
经检验点 因此Q点的轨迹方程为a2x2-b2y2=a4(除点(-a,0),(a,0)外) (1)解法二:设P(x0,y0),Q(x,y),∵A(-a,0),B(a ,0),QB⊥PB,QA⊥PA
(1)解法三:设P(x0,y0),Q(x,y),∵PA⊥QA ∴ 连接PQ,取PQ中点R
|

练习册系列答案
相关题目
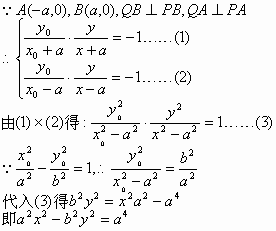
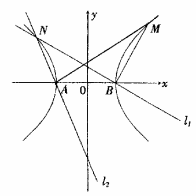


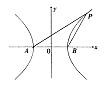
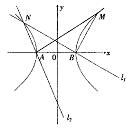
 (a>0,b>0),A、B为其左、右两个顶点,P是双曲线C1上的任意一点,作QB⊥PB,QA⊥PA,垂足分别为A、B,AQ与BQ交于点Q.
(a>0,b>0),A、B为其左、右两个顶点,P是双曲线C1上的任意一点,作QB⊥PB,QA⊥PA,垂足分别为A、B,AQ与BQ交于点Q.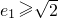 时,求e2的取值范围.
时,求e2的取值范围. (a>0,b>0),A、B为其左、右两个顶点,P是双曲线C1上的任意一点,作QB⊥PB,QA⊥PA,垂足分别为A、B,AQ与BQ交于点Q.
(a>0,b>0),A、B为其左、右两个顶点,P是双曲线C1上的任意一点,作QB⊥PB,QA⊥PA,垂足分别为A、B,AQ与BQ交于点Q.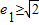 时,求e2的取值范围.
时,求e2的取值范围.