题目内容
命题p:?α∈R,sin(π-α)=cosα;命题q:函数y=lg(
+x)为奇函数.
现有如下结论:
①p是假命题; ②¬p是真命题; ③p∧q是假命题; ④¬p∨q是真命题.
其中结论说法错误的序号为
| x2+1 |
现有如下结论:
①p是假命题; ②¬p是真命题; ③p∧q是假命题; ④¬p∨q是真命题.
其中结论说法错误的序号为
①②③
①②③
.分析:先判断命题p,q的真假,利用复合命题与简单命题之间的关系进行判断.
解答:解:当α=
时,sin(π-
)=sin
=
,cos
=
,∴?α∈R,sin(π-α)=cosα,即p为真命题.
函数y=lg(
+x)的定义域为R,
则f(-x)+f(x)=lg(
-x)+lg(
+x)=lg((
-x)(
+x))=lg(x2+1-x2)=lg1=0,
∴f(-x)=-f(x),即函数y=lg(
+x)为奇函数正确.∴命题q为真命题.
故①p是假命题,错误.②¬p是真命题,错误.③p∧q是假命题,错误.④¬p∨q是真命题,正确.
故错误的是①②③,
故答案为:①②③.
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
函数y=lg(
| x2+1 |
则f(-x)+f(x)=lg(
| x2+1 |
| x2+1 |
| x2+1 |
| x2+1 |
∴f(-x)=-f(x),即函数y=lg(
| x2+1 |
故①p是假命题,错误.②¬p是真命题,错误.③p∧q是假命题,错误.④¬p∨q是真命题,正确.
故错误的是①②③,
故答案为:①②③.
点评:本题主要考查复合命题与简单命题之间的真假关系,先判断命题p,q的真假是解决本题的关键.

练习册系列答案
相关题目
 ),
),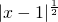 .则以下四个命题对已知的三个函数都能成立的是
.则以下四个命题对已知的三个函数都能成立的是 )
) ;
; 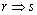 B.p:
B.p: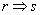 q:
q: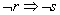
 q:
q:  D. p:
D. p: q:
q: