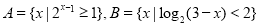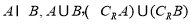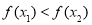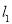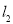题目内容
一次函数 是
是 上的增函数,
上的增函数, ,已知
,已知 .
.
(1)求 ;
;
(2)若 在
在 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;
(3)当 时,
时, 有最大值
有最大值 ,求实数
,求实数 的值.
的值.
(1)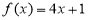 ;(2)
;(2)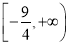 ;(3)
;(3) 或
或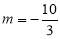 .
.
【解析】
试题分析:(1)先设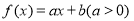 ,然后由
,然后由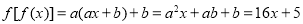 恒成立得方程组
恒成立得方程组 ,求解方程组即可,注意取
,求解方程组即可,注意取 的解;(2)由(1)得
的解;(2)由(1)得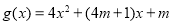 ,根据二次函数的图像与性质可知,要使
,根据二次函数的图像与性质可知,要使 在
在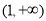 单调递增,只须该函数的对称轴大于或于1即可;(3)这是二次函数中定区间,而轴不定的最值问题,结合函数的图像,分对称轴在定区间的中点的左边、对称轴在定区间的中点的右边两种情况进行分类求解即可.
单调递增,只须该函数的对称轴大于或于1即可;(3)这是二次函数中定区间,而轴不定的最值问题,结合函数的图像,分对称轴在定区间的中点的左边、对称轴在定区间的中点的右边两种情况进行分类求解即可.
试题解析:(1)∵ 是
是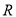 上的增函数,∴设
上的增函数,∴设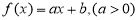 1分
1分

∴ 3分
3分
解得 或
或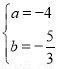 (不合题意舍去) 5分
(不合题意舍去) 5分
∴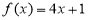 6分
6分
(2)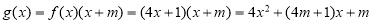 7分
7分
对称轴 ,根据题意可得
,根据题意可得 8分
8分
解得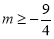
∴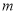 的取值范围为
的取值范围为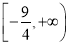 9分
9分
(3)①当 时,即
时,即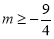 时
时
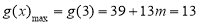 ,解得
,解得 ,符合题意 11分
,符合题意 11分
②当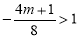 时,即
时,即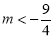 时
时
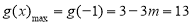 ,解得
,解得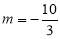 ,符合题意 13分
,符合题意 13分
由①②可得 或
或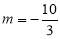 14分.
14分.
考点:1.函数的解析式;2.二次函数的图像与性质;3.函数的单调性与最值.

练习册系列答案
相关题目
某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第 | 1 | 2 | 3 | 4 | 5 |
被感染的计算机数量 | 10 | 20 | 39 | 81 | 160 |
则下列函数模型中能较好地反映计算机在第 天被感染的数量
天被感染的数量 与
与 之间的关系的是 ( )
之间的关系的是 ( )
A. B.
B. C.
C. D.
D.