题目内容
已知F是椭圆5x2+9y2=45的左焦点，P是此椭圆上的动点，A（1，1）是一定点，则|PA|+|PF|的最大值是 ．
【答案】分析：根据椭圆的第一定义可知|PA|+|PF|=|PA|+2a-|PF2|，|PA|+|PF|取得最大值时，即|PA|-|PF2|最大，结合图象可求出所求．
解答：解：椭圆5x2+9y2=45的标准方程为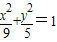
根据椭圆的第一定义：|PA|+|PF|=|PA|+2a-|PF2|
∴|PA|+|PF|取得最大值时，
即|PA|-|PF2|最大，
如图所示：|PA|+|PF|≤2a+|AF2|=6+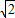
，
当P，A，F2共线时取得最大值．
∴|PA|+|PF|的最大值为：6+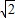
故答案为：6+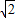
点评：本题主要考查了椭圆的定义，以及作图的能力，同时考查了运算求解的能力，属于基础题．
解答：解：椭圆5x2+9y2=45的标准方程为
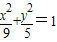
根据椭圆的第一定义：|PA|+|PF|=|PA|+2a-|PF2|
∴|PA|+|PF|取得最大值时，
即|PA|-|PF2|最大，
如图所示：|PA|+|PF|≤2a+|AF2|=6+
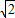，当P，A，F2共线时取得最大值．
∴|PA|+|PF|的最大值为：6+
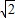
故答案为：6+
点评：本题主要考查了椭圆的定义，以及作图的能力，同时考查了运算求解的能力，属于基础题．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
的最小值，并求相应点P的坐标；