题目内容
已知F是椭圆5x2+9y2=45的右焦点,P为该椭圆上的动点,A(2,1)是一定点.(1)求
 的最小值,并求相应点P的坐标;
的最小值,并求相应点P的坐标;(2)求|PA|+|PF|的最大值与最小值;
(3)过点F作倾斜角为60°的直线交椭圆于M、N两点,求|MN|;
(4)求过点A且以A为中点的弦所在的直线方程.
【答案】分析:(1)由题意可得: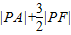 =
=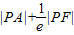 ,进而根据椭圆的第二定义可得:过A作右准线的垂线,交与B点,则
,进而根据椭圆的第二定义可得:过A作右准线的垂线,交与B点,则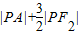 的最小值为|AB|,即可得到答案.
的最小值为|AB|,即可得到答案.
(2)根据椭圆的第一定义:|PA|+|PF1|=2a+|PA|-|PF2|,结合图形可得||PA|-|PF2||≤|AF2|=1⇒-1≤|PA|-|PF2|≤1,即可解决问题.
(3)设出直线的方程,联立直线与椭圆的方程利用由弦长公式可得答案.
(4)设出直线方程代入椭圆的方程进行化简,再结合根与系数的关系可得答案.
解答:解:(1)由题意可得:e=
所以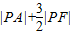 =
=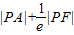 ,
,
∴根据椭圆的第二定义:过A作右准线的垂线,交与B点,则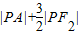 的最小值为|AB|,
的最小值为|AB|,
∵|AB|=
∴,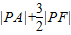 的最小值
的最小值 ,并且P(
,并且P(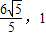 ).
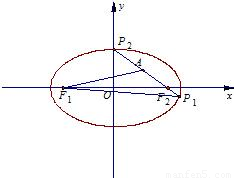
).
(2)根据椭圆的第一定义:|PA|+|PF1|=2a+|PA|-|PF2|
如图所示:因为||PA|-|PF2||≤|AF2|=1⇒-1≤|PA|-|PF2|≤1,
所以5<6+|PA|-|PF2|<7,即5<|PA|+|PF1|<7,
所以PA|+|PF|的最大值与最小值分别为5,7.
(3)由题意可得:直线方程为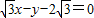 ,
,
联立直线与椭圆的方程可得:32x2-108x+63=0,
所以x1+x2=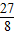 ,x1•x2=
,x1•x2=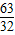 ,
,
由弦长公式可得:|MN|=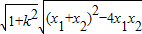 =
=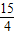 .
.
(4)由题意得,斜率存在,设为 k,则直线l的方程为 y-1=k(x-2),
代入椭圆的方程化简得:(5+9k2)x2+18k(1-2k)x+9(1-2k)2-45=0,
因为A为弦的中点,
所以x1+x2=4,即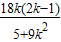 =4,解得k=
=4,解得k=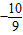 ,
,
所以以A为中点的弦所在的直线方程为10x+9y-29=0.
点评:本题主要考查了椭圆的应用以及椭圆中线段的最值问题,求解时要充分利用椭圆的定义可使得解答简洁,并且还考查了弦长问题与弦中点问题.
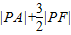 =
=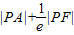 ,进而根据椭圆的第二定义可得:过A作右准线的垂线,交与B点,则
,进而根据椭圆的第二定义可得:过A作右准线的垂线,交与B点,则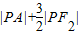 的最小值为|AB|,即可得到答案.
的最小值为|AB|,即可得到答案.(2)根据椭圆的第一定义:|PA|+|PF1|=2a+|PA|-|PF2|,结合图形可得||PA|-|PF2||≤|AF2|=1⇒-1≤|PA|-|PF2|≤1,即可解决问题.
(3)设出直线的方程,联立直线与椭圆的方程利用由弦长公式可得答案.
(4)设出直线方程代入椭圆的方程进行化简,再结合根与系数的关系可得答案.
解答:解:(1)由题意可得:e=

所以
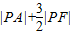 =
=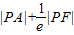 ,
,∴根据椭圆的第二定义:过A作右准线的垂线,交与B点,则
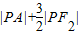 的最小值为|AB|,
的最小值为|AB|,∵|AB|=

∴,
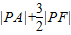 的最小值
的最小值 ,并且P(
,并且P(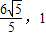 ).
).
(2)根据椭圆的第一定义:|PA|+|PF1|=2a+|PA|-|PF2|
如图所示:因为||PA|-|PF2||≤|AF2|=1⇒-1≤|PA|-|PF2|≤1,
所以5<6+|PA|-|PF2|<7,即5<|PA|+|PF1|<7,
所以PA|+|PF|的最大值与最小值分别为5,7.
(3)由题意可得:直线方程为
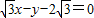 ,
,联立直线与椭圆的方程可得:32x2-108x+63=0,
所以x1+x2=
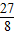 ,x1•x2=
,x1•x2=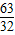 ,
,由弦长公式可得:|MN|=
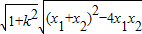 =
=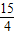 .
.(4)由题意得,斜率存在,设为 k,则直线l的方程为 y-1=k(x-2),
代入椭圆的方程化简得:(5+9k2)x2+18k(1-2k)x+9(1-2k)2-45=0,
因为A为弦的中点,
所以x1+x2=4,即
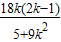 =4,解得k=
=4,解得k=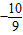 ,
,所以以A为中点的弦所在的直线方程为10x+9y-29=0.
点评:本题主要考查了椭圆的应用以及椭圆中线段的最值问题,求解时要充分利用椭圆的定义可使得解答简洁,并且还考查了弦长问题与弦中点问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目