题目内容
函数 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当 时,
时, 成立,若
成立,若 ,
, ,则
,则 大小关系 ( )
大小关系 ( )
A. | B. | C. | D. |
A
解析试题分析:设F(x)=xf(x),得F'(x)=x'f(x)+xf'(x)=xf'(x)+f(x),∵当x∈(-∞,0)时,xf′(x)<f(-x),且f(-x)=-f(x),∴当x∈(-∞,0)时,xf′(x)+f(x)<0,即F'(x)<0,由此可得F(x)=xf(x)在区间(-∞,0)上是减函数,∵函数y=f(x)是定义在实数集R上的奇函数,∴F(x)=xf(x)是定义在实数集R上的偶函数,在区间(0,+∞)上F(x)=xf(x)是增函数.∵0<lg3<lg10=1,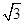 ∈(1,2),∴F(2)>F(
∈(1,2),∴F(2)>F(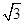 )>F(lg3),∵
)>F(lg3),∵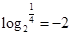 ,从而F(
,从而F(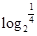 )=F(-2)=F(2),∴F(
)=F(-2)=F(2),∴F(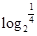 )>F(
)>F(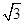 )>F(lg3),即(
)>F(lg3),即(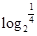 )f(
)f(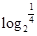 )>
)>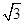 f(
f(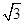 )>(lg3)f(lg3),得c>a>b,故答案为:A
)>(lg3)f(lg3),得c>a>b,故答案为:A
考点:本题考查了函数的性质
点评:本题给出抽象函数,比较几个函数值的大小.着重考查了利用导数研究函数的单调性、不等式比较大小和函数单调性与奇偶性关系等知识,属于中档题

练习册系列答案
相关题目
下列函数求导数,正确的个数是 ( )
①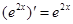 ;②
;②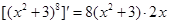 ;③
;③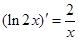 ;④
;④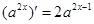
| A.0 | B.1 | C.2 | D.3 |
已知定义在 上的函数
上的函数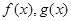 满足
满足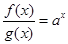 ,且
,且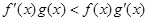 ,
,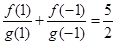 ,若数列
,若数列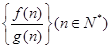 的前
的前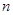 项和等于
项和等于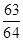 ,则
,则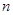 =
=
| A.7 | B.6 | C.5 | D.4 |
已知函数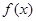 在R上可导,且
在R上可导,且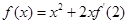 ,则
,则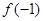 与
与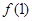 的大小为( )
的大小为( )
A.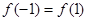 | B.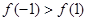 |
C.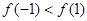 | D.不确定 |
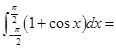 ( )
( )
A. | B.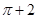 | C.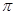 | D.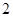 |
曲线 在点P(1,12)处的切线与两坐标轴围成三角形的面积是
在点P(1,12)处的切线与两坐标轴围成三角形的面积是
| A.75 | B. | C.27 | D. |
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
| A.-1<a<2 | B.-3<a<6 | C.a<-1或a>2 | D.a<-3或a>6 |
函数 的导数是( )
的导数是( )
A. | B. | C. | D. |
曲线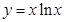 在点
在点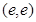 处的切线与直线
处的切线与直线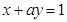 垂直,则实数
垂直,则实数 的值为 ( )
的值为 ( )
A.2  | B.-2 | C. | D.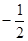 |