题目内容
17.离心率$e=\frac{2}{3}$,焦距2c=4的椭圆的标准方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1或$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{5}$=1.分析 由椭圆的焦距是4,离心率$e=\frac{2}{3}$,先求出a=3,c=2,可得b,分焦点在x轴和y轴,求出椭圆的标准方程.
解答 解:∵椭圆的焦距是4,离心率$e=\frac{2}{3}$,
∴c=2,$\frac{c}{a}$=$\frac{2}{3}$,解得a=3,
b2=a2-c2=9-4=5,
∴当焦点在x轴上,椭圆的标准方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1;
当焦点在y轴上,椭圆的标准方程为$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{5}$=1.
故答案为:$\frac{x^2}{9}+\frac{y^2}{5}=1$或$\frac{y^2}{9}+\frac{x^2}{5}=1$.
点评 本题考查椭圆的标准方程的求法,注意运用椭圆的性质,是基础题,解题时要避免丢解.

练习册系列答案
相关题目
9.已知有三个数a=($\frac{11}{3}$)-2,b=40.3,c=80.25,则它们之间的大小关系是( )
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |
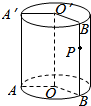 如图,圆柱OO′的底面半径为2cm,高为4cm,且P为母线B′B的重点,∠AOB=120°,则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\frac{2}{3}\sqrt{4{π}^{2}+9}$.
如图,圆柱OO′的底面半径为2cm,高为4cm,且P为母线B′B的重点,∠AOB=120°,则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\frac{2}{3}\sqrt{4{π}^{2}+9}$. 已知如图,在Rt△ABC中,∠A=60°,AB=6,点D、E是斜边AB上两点.
已知如图,在Rt△ABC中,∠A=60°,AB=6,点D、E是斜边AB上两点.