Question

若f(1)=0，f(0)=f(1×0)=f(1)f(0)=0，所以f(1)=f(0)与已知条件“”矛盾所以f(1)≠0，因此f(1)=1,所以f(1)-1=0，1是函数y=f(x)-1的零点

（2）因为f(1)=f[(-1)×（-1）]=f2(-1)=,所以f(-1)=±1，但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1，只能等于-1。所以任x∈R，f(-x)=f(-1)f(x)=-f(x)，因此函数是奇函数

已知某地每单位面积的菜地年平均使用氮肥量与每单位面积蔬菜年平均产量之间有的关系如下数据：

年份	x(kg)	y(t)
1985	70	5.1
1986	74	6.0
1987	80	6.8
1988	78	7.8
1989	85	9.0
1990	92	10.2
1991	90	10.0
1992	95	12.0
1993	92	11.5
1994	108	11.0
1995	115	11.8
1996	123	12.2
1997	130	12.5
1998	138	12.8
1999	145	13.0

(1)求x与y之间的相关系数，并检验是否线性相关；

（2）若线性相关，则求蔬菜产量y与使用氮肥x之间的回归直线方程，并估计每单位面积施150kg时，每单位面积蔬菜的平均产量.

Answer 1

见解析

解析:

若设，则

所以变量对变量的回归方程是

若f(1)=0，f(0)=f(1×0)=f(1)f(0)=0，所以f(1)=f(0)与已知条件“”矛盾所以f(1)≠0，因此f(1)=1,所以f(1)-1=0，1是函数y=f(x)-1的零点

（2）因为f(1)=f[(-1)×（-1）]=f2(-1)=,所以f(-1)=±1，但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1，只能等于-1。所以任x∈R，f(-x)=f(-1)f(x)=-f(x)，因此函数是奇函数

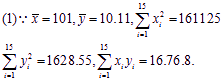 故蔬菜产量与使用氮肥量的相关系数为：

由于，故自由度为15－2＝13，由相关系数检验的临界值表查出与显著水平0.05及自由度13相关系数临界值从而可以看出，从而说明蔬菜产量与氮肥使用量之间存在相关关系.

（2）设所求的回归直线方程为：，则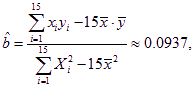

从而所求的回归直线方程为：

所以当时，

即估计每单位面积施肥150（t）时，每单位面积蔬菜的年平均产量为