题目内容
已知函数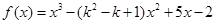 ,
,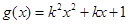 ,其中
,其中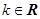 .
.
(1)设函数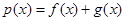 ,若
,若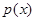 在区间
在区间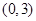 是单调函数,求
是单调函数,求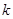 的取值范围;
的取值范围;
(2)设函数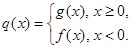 ,是否存在
,是否存在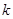 ,对任意给定的非零实数
,对任意给定的非零实数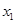 ,存在惟一的非零实数
,存在惟一的非零实数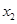 (
(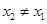 ),使得
),使得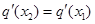 成立?若存在,求
成立?若存在,求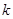 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
解:(1)因 ……1分
……1分
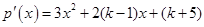 , ∵
, ∵ 在区间
在区间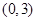 上单调
上单调 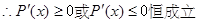
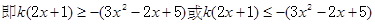 恒成立 ……2分
恒成立 ……2分
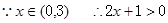
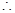
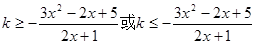 恒成立
恒成立
设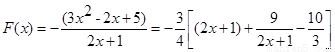
令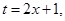 有
有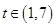 ,记
,记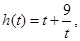
由函数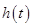 的图像可知,
的图像可知,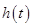 在
在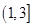 上单调递减,在
上单调递减,在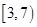 上单调递增,……4分
上单调递增,……4分
∴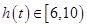 ,于是
,于是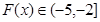 ……5分
……5分
∴ 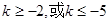 ……6分
……6分
(2)当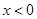 时有
时有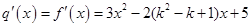 ; ……7分
; ……7分
当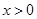 时有
时有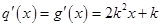 ,因为当
,因为当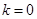 时不合题意,因此
时不合题意,因此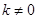 ,……8分
,……8分
下面讨论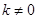 的情形,
的情形,
记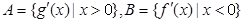 求得
A
求得
A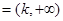 ,B=
,B=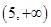
(ⅰ)当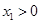 时,
时,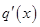 在
在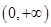 上单调递增,所以要使
上单调递增,所以要使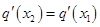 成立,只能
成立,只能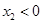 且
且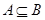 ,因此有
,因此有 ……9分
……9分
(ⅱ)当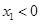 时,
时,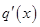 在
在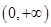 上单调递减,所以要使
上单调递减,所以要使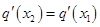 成立,只能
成立,只能 且
且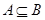 ,因此
,因此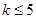 ……11分
……11分
综合(ⅰ)(ⅱ)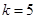 ……12分
……12分
当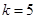 时A=B,则
时A=B,则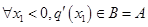 ,即
,即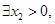 使得
使得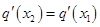 成立,
成立,
因为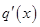 在
在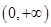 上单调递增,所以
上单调递增,所以 的值是唯一的;…13分
的值是唯一的;…13分
同理,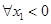 ,即存在唯一的非零实数
,即存在唯一的非零实数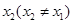 ,要使
,要使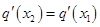 成立,
成立,
所以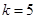 满足题意. …14分
满足题意. …14分
【解析】本试题主要是考查导数在研究函数中的运用。
(1)根据函数在给定区间单调递增,则可以利用导函数恒大于等于零,分离参数的思想求解参数的范围,
(2)分别分析函数f(x)和g(x)的性质得到单调性,进而确定是否存在点满足已知条件来求解得到。

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
 ,函数
,函数 ,
, ,(其中e是自然对数的底数,为常数),
,(其中e是自然对数的底数,为常数), 时,求
时,求 的单调区间与极值;
的单调区间与极值; ,使得
,使得 ,
, .(其中
.(其中 为自然对数的底数),
为自然对数的底数), 在
在 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值; ≥0,
≥0, 恒成立,试确定实数
恒成立,试确定实数 时,是否存在实数
时,是否存在实数 ,使曲线C:
,使曲线C: 在点
在点
 轴垂直?若存在,求出
轴垂直?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. ,
, ,其中
,其中
 是函数
是函数 的极值点,求实数
的极值点,求实数 的值
的值 (
( 为自然对数的底数)都有
为自然对数的底数)都有 ≥
≥ 成立,求实数
成立,求实数 ,
, (其中
(其中 )的周期为π,且图象上一个最低点为
)的周期为π,且图象上一个最低点为 。
。 的解析式;
的解析式; 时,求
时,求