题目内容
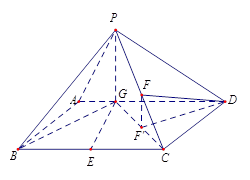
如图四棱锥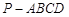 中,底面
中,底面 是平行四边形,
是平行四边形,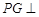 平面
平面 ,垂足为
,垂足为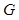 ,
,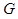 在
在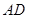 上且
上且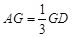 ,
,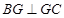 ,
,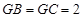 ,
,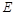 是
是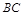 的中点,四面体
的中点,四面体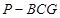 的体积为
的体积为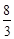 .
.
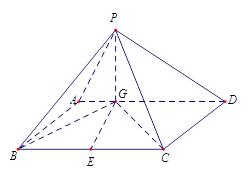
(1)求过点P,C,B,G四点的球的表面积;
(2)求直线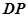 到平面
到平面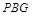 所成角的正弦值;
所成角的正弦值;
(3)在棱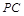 上是否存在一点
上是否存在一点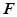 ,使
,使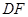
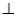
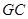 ,若存在,确定点
,若存在,确定点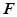 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
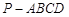 中,底面
中,底面 是平行四边形,
是平行四边形,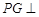 平面
平面 ,垂足为
,垂足为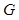 ,
,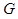 在
在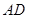 上且
上且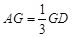 ,
,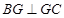 ,
,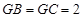 ,
,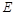 是
是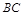 的中点,四面体
的中点,四面体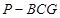 的体积为
的体积为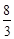 .
.
(1)求过点P,C,B,G四点的球的表面积;
(2)求直线
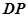 到平面
到平面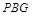 所成角的正弦值;
所成角的正弦值;(3)在棱
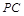 上是否存在一点
上是否存在一点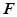 ,使
,使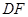
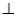
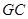 ,若存在,确定点
,若存在,确定点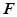 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.(1)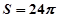 ;(2)
;(2)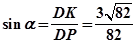 ;(3)存在,
;(3)存在,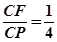 .
.
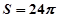 ;(2)
;(2)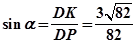 ;(3)存在,
;(3)存在,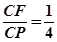 .
.试题分析:(1)首先由四面体
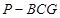 的体积可以求出高
的体积可以求出高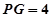 .
.因为
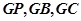 两两垂直,所以以
两两垂直,所以以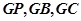 为同一顶点的三条棱构造长方体,长方体的外接球即为过点P,C,B,G四点的球,其直径就是长方体的体对角线.
为同一顶点的三条棱构造长方体,长方体的外接球即为过点P,C,B,G四点的球,其直径就是长方体的体对角线.(2)由于面
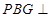 面
面 ,所以只需在面ABCD内过点D作交线BG的垂线,即可得PD在面PBG内的射影,从而得PD与面PBG所成的角. (3)首先假设
,所以只需在面ABCD内过点D作交线BG的垂线,即可得PD在面PBG内的射影,从而得PD与面PBG所成的角. (3)首先假设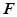 存在,然后确定
存在,然后确定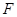 的位置,若能在
的位置,若能在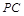 上找到点
上找到点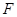 使
使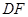
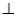
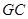 则说明这样的点F存在.
则说明这样的点F存在.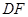 与
与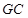 是异面的两条直线,我们通过转化,转化这相交的两条直线的垂直问题.那么如何转化?过
是异面的两条直线,我们通过转化,转化这相交的两条直线的垂直问题.那么如何转化?过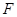 作
作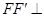
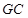 交GC于
交GC于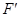 ,则只要
,则只要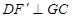 即可.这样确定
即可.这样确定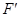 的位置容易得多了.
的位置容易得多了.试题解析:(1)由四面体
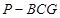 的体积为
的体积为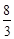 .∴
.∴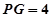 .
.以
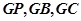 构造长方体,外接球的直径为长方体的体对角线。
构造长方体,外接球的直径为长方体的体对角线。∴
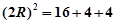 ∴
∴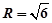
∴
 3分
3分(2)由
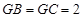
∴
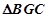 为等腰三角形,GE为
为等腰三角形,GE为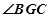 的角平分线,作
的角平分线,作 交BG的延长线于K,
交BG的延长线于K,∴

由平面几何知识可知:
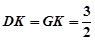 ,
,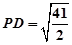 .设直线
.设直线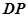 与平面
与平面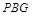 所成角为
所成角为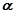
∴
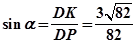 8分
8分(3)假设
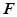 存在,过
存在,过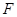 作
作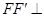
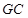 交GC于
交GC于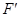 ,则必有
,则必有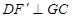 .因为
.因为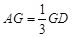 ,且
,且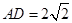 ,所以
,所以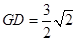 ,又
,又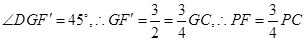 .
.
∴当
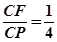 时满足条件 12分
时满足条件 12分
练习册系列答案
相关题目
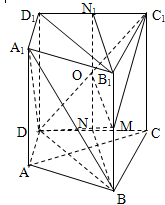
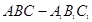 中,
中,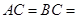
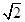 ,且
,且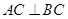 ,点
,点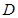 是
是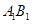 中点.
中点.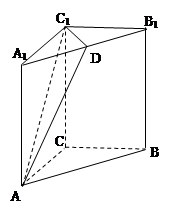
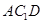 ⊥平面
⊥平面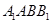 ;
;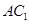 与平面
与平面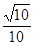 ,
,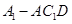 的体积.
的体积.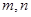 是两条不同的直线,
是两条不同的直线,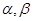 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( ) ,
,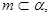
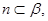 则
则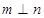
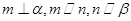 ,则
,则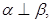
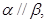
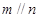
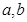 都在平面
都在平面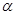 外, 则下列推断错误的是( )
外, 则下列推断错误的是( )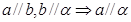
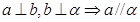
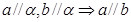
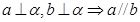
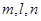 和平面
和平面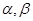 的四个命题:
的四个命题: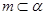 ,
,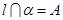 ,点
,点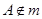 ,则
,则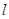 与
与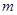 不共面;
不共面;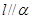 ,
,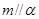 ,且
,且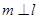 ,
,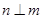 ,则
,则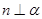 ;
;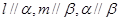 ,则
,则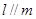 ;
;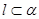 ,
,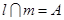 ,
,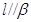 ,
,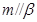 ,则
,则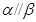 .
.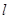 上有一点在平面
上有一点在平面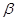 外,则
外,则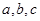 中,
中,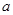 与
与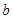 共面且
共面且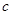 共面,则
共面,则