题目内容
设角α的终边过点P(-4a,3a) (a≠0),则2sinα+cosα的值是( )
分析:求出OP的距离,利用三角函数的定义,求出sinα,cosα,即可求解.
解答:解:因为角α的终边过点P(-4a,3a) (a≠0),
所以|OP|=5|a|=
,
当a>0时,sinα=
=
,cosα=
=-
.
所以2sinα+cosα=2×
-
=
.
当a<0时,sinα=-
=-
,cosα=
=
.
所以2sinα+cosα=-2×
+
=-
.
故选C.
所以|OP|=5|a|=
|
当a>0时,sinα=
| 3a |
| 5a |
| 3 |
| 5 |
| -4a |
| 5a |
| 4 |
| 5 |
所以2sinα+cosα=2×
| 3 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
当a<0时,sinα=-
| 3a |
| 5a |
| 3 |
| 5 |
| -4a |
| -5a |
| 4 |
| 5 |
所以2sinα+cosα=-2×
| 3 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
故选C.
点评:本题考查任意角的三角函数的定义,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的终边过点P
的终边过点P ,则
,则 的值是
的值是  (B)
(B)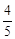 (C)
(C) (D)
(D)