题目内容
设角α的终边过点P(-6a,-8a)(a≠0),则sinα-cosα的值是分析:根据角α的终边过点P(-6a,-8a)(a≠0),可由三角函数定义先求出sinα与cosα的值,再作差.
解答:解:∵角α的终边过点P(-6a,-8a)(a≠0),
∴sinα=
=-
,cosα=
=-
,
∴sinα-cosα=-
当a>0时,sinα-cosα=-
,当a<0时,sinα-cosα=
故答案为:-
或
.
∴sinα=
| -8a | ||
|
| 4a |
| 5|a| |
| -6a | ||
|
| 3a |
| 5|a| |
∴sinα-cosα=-
| a |
| 5|a| |
当a>0时,sinα-cosα=-
| 1 |
| 5 |
| 1 |
| 5 |
故答案为:-
| 1 |
| 5 |
| 1 |
| 5 |
点评:本题主要考查已知角α的终边一点球三角函数值的问题.

练习册系列答案
相关题目
 的终边过点P
的终边过点P ,则
,则 的值是
的值是  (B)
(B)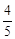 (C)
(C) (D)
(D)