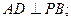题目内容
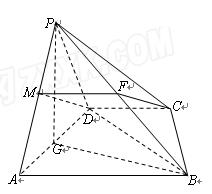
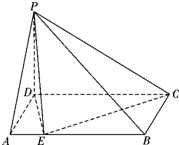
 图4,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,
图4,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,
∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD.
 |
(1)(2)见解析
解析:
(1)如图,连接AC,
∵ABCD为矩形且F是BD的中点,
 ∴AC必经过F 。
∴AC必经过F 。
又E是PC的中点,
所以,EF∥AP。
∵EF在面PAD外,PA在面内,
∴ EF∥面PAD
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD![]() 面ABCD=AD,
面ABCD=AD,
∴CD⊥面PAD, 8分
又AP![]() 面PAD,∴AP⊥CD. 9分
面PAD,∴AP⊥CD. 9分
又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD。
又AD![]() 面PAD,所以,面PDC⊥面PAD 。
面PAD,所以,面PDC⊥面PAD 。

练习册系列答案
相关题目
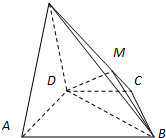
 (2012•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点.已知PD=
(2012•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点.已知PD= 已知如图4,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,
已知如图4,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2, 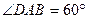 ,AB=AD=2CD,侧面
,AB=AD=2CD,侧面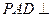 底面ABCD,且
底面ABCD,且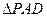 为等腰直角三角形,
为等腰直角三角形,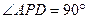 ,M为AP的中点。
,M为AP的中点。