Question

【题目】对任意实数x和任意，恒有，则实数a的取值范围为_____．

Answer 1

【答案】a或a

【解析】

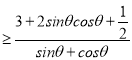原不等式等价于（3+2sinθcosθ﹣asinθ﹣acosθ）2，θ∈[0，]，从而可得a，或a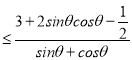，于是问题转化为求函数的最值问题加以解决，对上述分式进行合理变形，利用函数单调性、基本不等式即可求得最值．

原不等式等价于（3+2sinθcosθ﹣asinθ﹣acosθ）2，θ∈[0，]①，

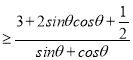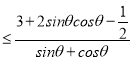由①得a②，或a③，

在②中，，

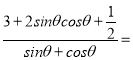（sinθ+cosθ），

显然当1≤x时，f（x）＝x为减函数，从而上式最大值为f（1）＝1，

由此可得a；

在③中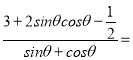，（sinθ+cosθ），

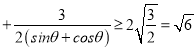当且仅当sinθ+cosθ时取等号，

所以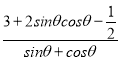的最小值为，

由此可得a，

综上，a或a．

故答案为：a或a．