题目内容
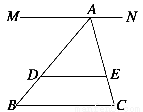
如图所示，在梯形ABCD中，已知AD∥BC，DC⊥BC，∠B＝60°，BC＝AB，E为AB的中点．
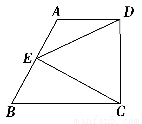
求证：△ECD为等边三角形．
见解析
【解析】
证明 过E作EF∥BC交DC于F，连接AC，如图所示．
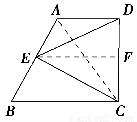
∵AD∥BC，E为AB中点，∴F是DC中点．①
又∵DC⊥BC，EF∥BC，∴EF⊥DC.②
∴由①②知，EF是DC的垂直平分线，
∴△ECD为等腰三角形．③
∵BC＝AB，∠B＝60°，∴△ABC是等边三角形．
又∵E是AB中点，
∴CE是∠ACB的平分线，
∴∠BCE＝30°.∴∠ECD＝60°.④
由③④知，△ECD为等边三角形．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
