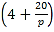题目内容
【题目】对于无穷数列![]() ,
,![]() ,若
,若![]() -
-![]()
![]() …,则称
…,则称![]() 是
是![]() 的“收缩数列”.其中,
的“收缩数列”.其中,![]() ,
,![]() 分别表示
分别表示![]() 中的最大数和最小数.已知
中的最大数和最小数.已知![]() 为无穷数列,其前
为无穷数列,其前![]() 项和为
项和为![]() ,数列
,数列![]() 是
是![]() 的“收缩数列”.
的“收缩数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() ;
;
(3)若![]() ,求所有满足该条件的
,求所有满足该条件的![]() .
.
【答案】(1)![]() (2)证明见解析(3)所有满足该条件的数列
(2)证明见解析(3)所有满足该条件的数列![]() 为
为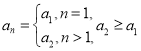
【解析】
(1)由![]() 可得
可得![]() 为递增数列,
为递增数列,![]() ,
,![]() ,从而易得
,从而易得![]() ;
;
(2)利用![]() ,
,
![]() ,可证
,可证![]() 是不减数列(即
是不减数列(即![]() ),而
),而![]() ,由此可得
,由此可得![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() .
.
(3)首先,由已知,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() (*),这里分析
(*),这里分析![]() 与
与![]() 的大小关系,
的大小关系,![]() ,
,![]() 均出现矛盾,
均出现矛盾,![]() ,结合(*)式可得
,结合(*)式可得![]() ,因此猜想
,因此猜想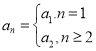 (
(![]() ),用反证法证明此结论成立,证明时假设
),用反证法证明此结论成立,证明时假设![]() 是首次不符合
是首次不符合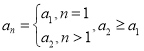 的项,则
的项,则![]() ,这样题设条件变为
,这样题设条件变为![]() (*),仿照讨论
(*),仿照讨论![]() 的情况讨论
的情况讨论![]() ,可证明.
,可证明.
解:(1)由![]() 可得
可得![]() 为递增数列,
为递增数列,
所以![]() ,
,
故![]() 的前
的前![]() 项和为
项和为![]() .
.
(2)因为![]() ,
,
![]() ,
,
所以![]()
所以![]() .
.
又因为![]() ,所以
,所以![]() ,
,
所以![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() .
.
(3)由![]() 可得
可得
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() (*),
(*),
若![]() ,则
,则![]() ,所以由(*)可得
,所以由(*)可得![]() ,与
,与![]() 矛盾;
矛盾;
若![]() ,则
,则![]() ,所以由(*)可得
,所以由(*)可得![]() ,
,
所以![]() 与
与![]() 同号,这与
同号,这与![]() 矛盾;
矛盾;
若![]() ,则
,则![]() ,由(*)可得
,由(*)可得![]() .
.
猜想:满足![]() 的数列
的数列![]() 是:
是:
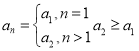 .
.
经验证,左式![]() ,
,
右式![]() .
.
下面证明其它数列都不满足(3)的题设条件.
法1:由上述![]() 时的情况可知,
时的情况可知,![]() 时,
时,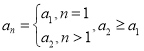 是成立的.
是成立的.
假设![]() 是首次不符合
是首次不符合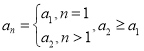 的项,则
的项,则![]() ,
,
由题设条件可得![]() (*),
(*),
若![]() ,则由(*)式化简可得
,则由(*)式化简可得![]() 与
与![]() 矛盾;
矛盾;
若![]() ,则
,则![]() ,所以由(*)可得
,所以由(*)可得![]()
所以![]() 与
与![]() 同号,这与
同号,这与![]() 矛盾;
矛盾;
所以![]() ,则
,则![]() ,所以由(*)化简可得
,所以由(*)化简可得![]() .
.
这与假设![]() 矛盾.
矛盾.
所以不存在数列不满足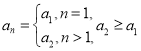 的
的![]() 符合题设条件.
符合题设条件.
法2:当![]() 时,
时,![]() ,
,
所以![]()
即![]()
由![]() 可得
可得![]()
又![]() ,所以可得
,所以可得![]() ,
,
所以![]() ,
,
即![]()
所以![]() 等号成立的条件是
等号成立的条件是
![]() ,
,
所以,所有满足该条件的数列![]() 为
为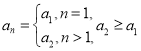 .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目