题目内容
已知数列 满足:
满足: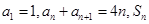 是数列
是数列 的前n项和.数列
的前n项和.数列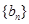 前n项的积为
前n项的积为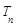 ,且
,且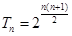
(Ⅰ)求数列 ,
,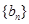 的通项公式;
的通项公式;
(Ⅱ)是否存在常数a,使得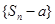 成等差数列?若存在,求出a,若不存在,说明理由;
成等差数列?若存在,求出a,若不存在,说明理由;
(Ⅲ)是否存在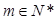 ,满足对任意自然数
,满足对任意自然数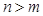 时,
时,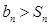 恒成立,若存在,求出m的值;若不存在,说明理由.
恒成立,若存在,求出m的值;若不存在,说明理由.
(Ⅰ) ,
, ;(Ⅱ)不存在;(Ⅲ)
;(Ⅱ)不存在;(Ⅲ) .
.
解析试题分析:(Ⅰ)由条件可得数列 隔项成等差数列,从而分别得到n为奇数和偶数时的通项公式,合并即得数列
隔项成等差数列,从而分别得到n为奇数和偶数时的通项公式,合并即得数列 的通项公式.再由数列
的通项公式.再由数列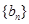 前n项的积为
前n项的积为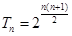 ,由
,由 再验证
再验证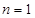 时的情况,即可得到
时的情况,即可得到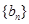 的通项公式;(Ⅱ)先求出
的通项公式;(Ⅱ)先求出 的表达式,再假设
的表达式,再假设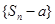 成等差数列,由等差中项的知识,
成等差数列,由等差中项的知识, ,代入发现等式恒不成立,从而得到不存在常数a 使数列
,代入发现等式恒不成立,从而得到不存在常数a 使数列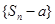 成等差数列的结论;(Ⅲ)由上问可知即证明存在
成等差数列的结论;(Ⅲ)由上问可知即证明存在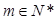 ,满足对任意自然数
,满足对任意自然数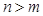 时,
时, ,易知存在m=4使得当
,易知存在m=4使得当 时,
时,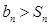 恒成立.接着用数学归纳法证明之.
恒成立.接着用数学归纳法证明之.
试题解析:(Ⅰ)由题知 ,∴
,∴ ,∴
,∴
即数列 隔项成等差数列, 1分
隔项成等差数列, 1分
又
∴当n为奇数时,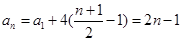 ,
,
当n为偶数时,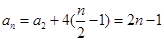 2分
2分
∴对一切 3分
3分
又 ,当
,当 时
时 ,且
,且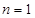 时满足上式,
时满足上式,
∴对一切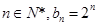 5分
5分
(Ⅱ)由(Ⅰ)知 ,数列
,数列 成等差数列,∴
成等差数列,∴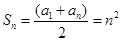
∴ 7分
7分
若存在常数a,使得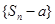 成等差数列,则
成等差数列,则 在
在 时恒成立
时恒成立
即
∴不存在常数a 使数列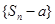 成等差数列 9分
成等差数列 9分
(Ⅲ)存在 使得当
使得当 时,
时,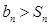 恒成立,
恒成立,
即当 时,
时, ,下面用用数学归纳法证明:
,下面用用数学归纳法证明:
①当 时,
时, .
.
②假设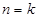 时,
时, 成立,即
成立,即 .
.
则当 ,
, ,所以
,所以 时,
时, 成立.
成立.
综合①②得, 成立.所以当
成立.所以当 时,
时, . 13分
. 13分
考点:1.等差数列通项公式;2.等差中项;3.数学归纳法.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
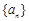 的前n项和为
的前n项和为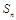 ,且
,且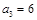 ,
,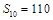 .
. 的通项公式;
的通项公式;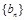 前n项和为
前n项和为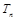 ,且
,且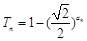 ,令
,令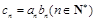 .求数列
.求数列 的前n项和
的前n项和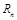 .
. 为等比数列,
为等比数列,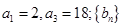 是等差数列,
是等差数列,
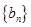 的通项公式及前
的通项公式及前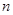 项和
项和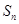 ;
;
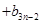 ,
,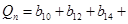
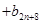 ,其中
,其中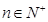 ,试比较
,试比较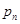 与
与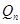 的大小,并加以证明.
的大小,并加以证明.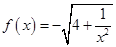 ,数列
,数列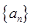 的前
的前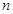 项和为
项和为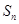 ,点
,点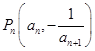 在曲线
在曲线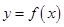 上
上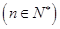 ,且
,且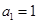 ,
,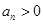 .
.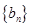 的前
的前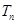 ,且满足
,且满足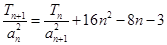 ,
,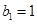 ,求数列
,求数列 ,
,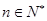 .
. 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
,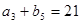 ,
,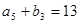 .
. 的前
的前 项和
项和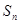 .
. 的首项
的首项 ,
, ,前
,前 项和为
项和为 .
. 及
及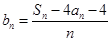 ,
, ,求
,求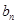 的最大值.
的最大值.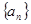 前
前 项和
项和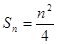 ,数列
,数列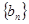 满足
满足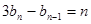 (
( ),
),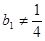 时,数列
时,数列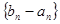 为等比数列;
为等比数列; ,若数列
,若数列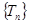 中只有
中只有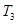 最小,求
最小,求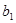 的取值范围.
的取值范围.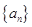 的前
的前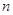 项和为
项和为 ,
,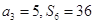 .
. 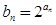 ,求数列
,求数列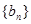 的前
的前 项和
项和 .
.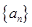 和等比数列
和等比数列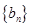 中,a1=2, 2b1=2, b6=32,
中,a1=2, 2b1=2, b6=32, 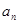 和
和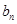 ;
;