题目内容
19.在△ABC中,已知tanA=2,tanB=3,∠A的对边a=1.(1)求∠C的大小;
(2)求△ABC的面积S.
分析 (1)利用两角和与差的正切函数公式求出tanC的值,即可确定出C的度数;
(2)由tanA与tanB的值,利用同角三角函数间的基本关系求出sinA与cosA的值,再由a的值,利用正弦定理求出b的值,利用三角形面积公式即可求出三角形ABC面积.
解答 解:(1)∵tanA=2,tanB=3,
∴tanC=-tan(A+B)=-$\frac{tanA+tanB}{1-tanAtanB}$=-$\frac{2+3}{1-6}$=1,
∵tanC<tanA<tanB,
∴∠C<∠A<∠B,
则∠C=45°;
(2)∵tanA=2,tanB=3,
∴cosA=$\sqrt{\frac{1}{1+ta{n}^{2}A}}$=$\frac{\sqrt{5}}{5}$,cosB=$\sqrt{\frac{1}{1+ta{n}^{2}B}}$=$\frac{\sqrt{10}}{10}$,
∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{2\sqrt{5}}{5}$,sinB=$\frac{3\sqrt{10}}{10}$,
∵a=1,
∴由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$得:b=$\frac{asinB}{sinA}$=$\frac{1×\frac{3\sqrt{10}}{10}}{\frac{2\sqrt{5}}{5}}$=$\frac{3\sqrt{6}}{4}$,
则S△ABC=$\frac{1}{2}$absinC=$\frac{3\sqrt{3}}{8}$.
点评 此题考查了正弦、余弦定理,同角三角函数间的基本关系,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
9.函数f(x)的定义域为[0,1),则f(1-3x)的定义域是( )
| A. | (-2,1] | B. | (-$\frac{1}{2}$,1] | C. | (0,$\frac{1}{3}$] | D. | (-$\frac{1}{3}$,0] |
14.在区间[-1,5]上任取一个数x,则log2(x+3)≥log2(3x+4)-1的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
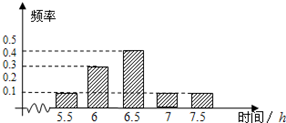 某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示.
某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示.