题目内容
设x1、x2(x1≠x2)是函数f(x)=ax3+bx2-a2x(a>0)的两个极值点.(1)若x1=-1,x2=2,求函数f(x)的解析式;
(2)若
 ,求b的最大值..
,求b的最大值..
【答案】分析:(1)由f(x)=ax3+bx2-a2x(a>0),知f'(x)=3ax2+2bx-a2(a>0)依题意有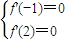 ,由此能求出f(x).
,由此能求出f(x).
(2)由f'(x)=3ax2+2bx-a2(a>0),知x1,x2是方程f'(x)=0的两个根,且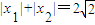 ,故(x1+x2)2-2x1x2+2|x1x2|=8.由此能求出b的最大值.
,故(x1+x2)2-2x1x2+2|x1x2|=8.由此能求出b的最大值.
解答:解:(1)∵f(x)=ax3+bx2-a2x(a>0),
∴f'(x)=3ax2+2bx-a2(a>0)
依题意有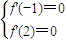 ,
,
∴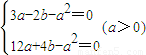 .
.
解得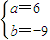 ,
,
∴f(x)=6x3-9x2-36x..
(2)∵f'(x)=3ax2+2bx-a2(a>0),
依题意,x1,x2是方程f'(x)=0的两个根,
且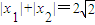 ,
,
∴(x1+x2)2-2x1x2+2|x1x2|=8.
∴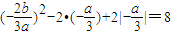 ,
,
∴b2=3a2(6-a)
∵b2≥0,
∴0<a≤6设p(a)=3a2(6-a),
则p′(a)=-9a2+36a.
由p'(a)>0得0<a<4,
由p'(a)<0得a>4.
即:函数p(a)在区间(0,4]上是增函数,
在区间[4,6]上是减函数,
∴当a=4时,p(a)有极大值为96,
∴p(a)在(0,6]上的最大值是96,
∴b的最大值为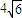 .
.
点评:本题考查函数解析式的求法和实数b的最大值的求法,对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.解题时要认真审题,仔细解答,注意导数性质的灵活运用.
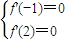 ,由此能求出f(x).
,由此能求出f(x).(2)由f'(x)=3ax2+2bx-a2(a>0),知x1,x2是方程f'(x)=0的两个根,且
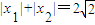 ,故(x1+x2)2-2x1x2+2|x1x2|=8.由此能求出b的最大值.
,故(x1+x2)2-2x1x2+2|x1x2|=8.由此能求出b的最大值.解答:解:(1)∵f(x)=ax3+bx2-a2x(a>0),
∴f'(x)=3ax2+2bx-a2(a>0)
依题意有
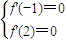 ,
,∴
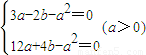 .
.解得
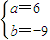 ,
,∴f(x)=6x3-9x2-36x..
(2)∵f'(x)=3ax2+2bx-a2(a>0),
依题意,x1,x2是方程f'(x)=0的两个根,
且
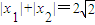 ,
,∴(x1+x2)2-2x1x2+2|x1x2|=8.
∴
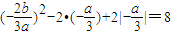 ,
,∴b2=3a2(6-a)
∵b2≥0,
∴0<a≤6设p(a)=3a2(6-a),
则p′(a)=-9a2+36a.
由p'(a)>0得0<a<4,
由p'(a)<0得a>4.
即:函数p(a)在区间(0,4]上是增函数,
在区间[4,6]上是减函数,
∴当a=4时,p(a)有极大值为96,
∴p(a)在(0,6]上的最大值是96,
∴b的最大值为
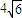 .
.点评:本题考查函数解析式的求法和实数b的最大值的求法,对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.解题时要认真审题,仔细解答,注意导数性质的灵活运用.

练习册系列答案
相关题目