题目内容
已知函数图象C′′与C:y(x+a+1)=ax+a2+1关于直线y=x对称,且图象C′关于点(2,-3)对称,则a的值为( )
分析:把已知函数变形,求出x,则原函数的反函数可求,整理后知反函数的图象的对称中心,由对称中心的坐标是(2,-3)可求a的值.
解答:解:由y(x+a+1)=ax+a2+1,得:x=
,
所以原函数的反函数为:y=
=
=
-a-1,
所以该函数图象关于(a,-a-1)中心对称,
又其关于(2,-3)对称,
所以a=2.
故选C.
| -ay-y+a2+1 |
| y-a |
所以原函数的反函数为:y=
| -ax-x+a2+1 |
| x-a |
| -(a+1)(x-a)-a+1 |
| x-a |
| -a+1 |
| x-a |
所以该函数图象关于(a,-a-1)中心对称,
又其关于(2,-3)对称,
所以a=2.
故选C.
点评:本题考查了函数反函数的求法,训练了函数对称中心的求解方法,考查了函数图象的平移变化.

练习册系列答案
相关题目
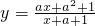 关于直线y=x对称,且图象C'关于(2,-3)对称,则a的值为________.
关于直线y=x对称,且图象C'关于(2,-3)对称,则a的值为________. 关于直线y=x对称,且图象C'关于(2,-3)对称,则a的值为 .
关于直线y=x对称,且图象C'关于(2,-3)对称,则a的值为 .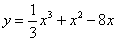 图象C上存在一定点P满足:若过P的直线
图象C上存在一定点P满足:若过P的直线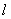 与曲线C交与不同于P的两点
与曲线C交与不同于P的两点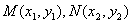 ,则恒有
,则恒有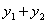 为定值
为定值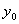 ,则
,则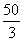 B.
B. 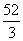 C.
C.
 D.
D.