题目内容
已知数列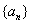 的前n项之和为
的前n项之和为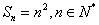 .
.
(1)求数列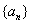 的通项公式;
的通项公式;
(2)设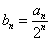 ,求数列
,求数列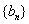 的前n项和Tn;
的前n项和Tn;
(3)求使不等式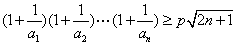 对一切n∈N*均成立的最大实教p.
对一切n∈N*均成立的最大实教p.
【答案】
解(1)当n≥2时, .
.
而a1=1符合n≥2时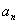 的形式,因此
的形式,因此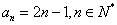 . …………2分
. …………2分
 …………7分
…………7分
(3)由题意得 对任意n∈N*恒成立.
对任意n∈N*恒成立.
设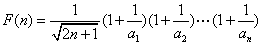 ,则
,则
 …………10分
…………10分
显然F(n)>0,因此,F(n+1)>F( n),即F(n)随着n的增大而增大.
所以F(n)的最小值是 .
.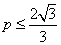 ,即最大实数P为
,即最大实数P为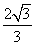 .……12分
.……12分
注:(1)中不验证a1=1符合n≥2时an的形式,扣1分.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 的前n项之和
的前n项之和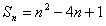 ,求数列
,求数列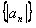 的前n项和Tn。
的前n项和Tn。  的前n项之和为10,则项数n为( )
的前n项之和为10,则项数n为( )