题目内容
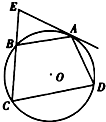 如图,四边形ABCD内接于⊙O,
如图,四边形ABCD内接于⊙O, |
| AB |
 |
| AD |
分析:根据圆的切线,得到圆周角等于同弧所对的弦切角,根据圆内接四边形的性质,得到一个内角等于不相邻的内角,有两个角相等,得到两个三角形相似,得到对应边成比例,把比例式转化为等式得到结果.
解答: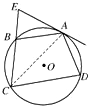 证明:连接AC,
证明:连接AC,
∵EA切⊙O于A,
∴∠EAB=∠ACB.
∵
=
,
∴∠ACD=∠ACB,AB=AD.
于是∠EAB=∠ACD.
又四边形ABCD内接于⊙O,
∴∠ABE=∠D.
∴△ABE∽△CDA.
于是
=
,即AB•DA=BE•CD.
∴AB2=BE•CD.
 证明:连接AC,
证明:连接AC,∵EA切⊙O于A,
∴∠EAB=∠ACB.
∵
 |
| AB |
 |
| AD |
∴∠ACD=∠ACB,AB=AD.
于是∠EAB=∠ACD.
又四边形ABCD内接于⊙O,
∴∠ABE=∠D.
∴△ABE∽△CDA.
于是
| AB |
| CD |
| BE |
| DA |
∴AB2=BE•CD.
点评:本题考查同弧所对的圆周角等于弦切角,考查圆内接四边形的性质,考查两个三角形相似的判定和性质,是一个比较简单的综合题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD.
如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD. 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= 如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.
如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=