题目内容
(本小题共13分)
如图所示,正方形 与矩形
与矩形 所在平面互相垂直,
所在平面互相垂直, ,点E为
,点E为 的中点。
的中点。
(Ⅰ)求证:
(Ⅱ) 求证:
(Ⅲ)在线段AB上是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
(1)根据三角形的中位线,那么可以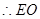 //
//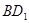 ,然后结合线面平行的判定定理可知结论。
,然后结合线面平行的判定定理可知结论。
(2)结合已知中正方形的心智,以及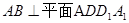 ,结合线面垂直的性质定理得到线线垂直。
,结合线面垂直的性质定理得到线线垂直。
(3)
解析试题分析:(Ⅰ)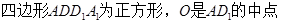 , 点E为
, 点E为 的中点,连接
的中点,连接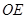 。
。
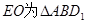 的中位线
的中位线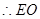 //
//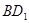 ……2分
……2分
又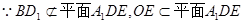
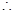
 ……4分
……4分
(II) 正方形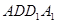 中,
中,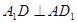
由已知可得: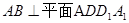 ,
, …….6分
…….6分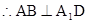 ,
, …….7分
…….7分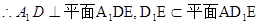
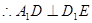 …….8分
…….8分
(Ⅲ)由题意可得: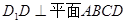 ,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则
,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则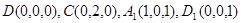 ,
, 9分
9分
设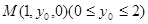
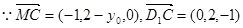 10分
10分
设平面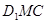 的法向量为
的法向量为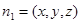
则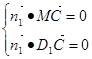
得 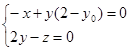 11分
11分
取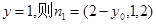 是平面
是平面 的一个法向量,而平面
的一个法向量,而平面 的一个法向量为
的一个法向量为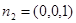 12分
12分
要使二面角 的大小为
的大小为
而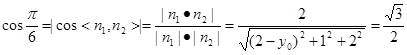
解得: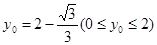
当 =
=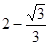 时,二面角
时,二面角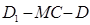 的大小为
的大小为
 13分
13分
考点:空间中的线面平行和线线垂直以及二面角的求解
点评:解决平行和垂直的证明,一般要用到判定定理和性质定理,然后结合空间向量法来求解二面角,属于基础题。

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
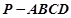 中,侧棱
中,侧棱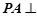 底面
底面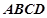 ,底面
,底面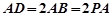 ,
,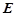 为
为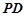 的上一点,且
的上一点,且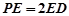 ,
, 为PC的中点.
为PC的中点.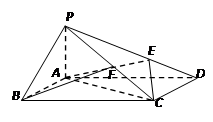

 平面AEC;
平面AEC;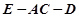 的余弦值.
的余弦值.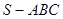 中,
中, 是边长为4的正三角形,
是边长为4的正三角形, ,
,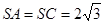 ,
,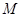 、
、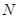 分别是
分别是 、
、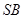 的中点;
的中点;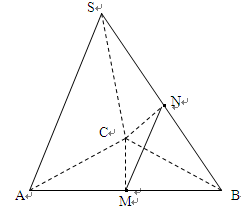

 平面
平面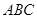 ;
;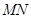 与平面
与平面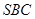 所成角的正弦值。
所成角的正弦值。 中,四边形
中,四边形 是菱形,
是菱形,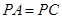 ,
, 为
为 的中点.
的中点.
 面
面 ; (2)求证:平面
; (2)求证:平面 平面
平面 .
.
 的底面
的底面 为平行四边形,
为平行四边形, 分别是棱
分别是棱 的中点,平面
的中点,平面 与平面
与平面 交于
交于 ,求证:
,求证:
 平面
平面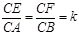 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 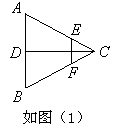
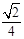 ,求k的值.
,求k的值. 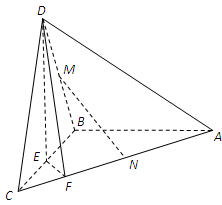
 中,底面
中,底面 是正方形.已知
是正方形.已知 ,
, .
.
 ;
; .
.