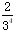Question

已知随机变量ξ的概率密度函数为 f(x)=

2x  ，0≤x≤1 0  ，x＜0或x＞1

，则P(

1

4

＜ξ＜

1

2

)=（　　）

• A．

  1

  4

• B．

  1

  7

• C．

  1

  9

• D．

  3

  16

Answer 1

分析：由随机变量ξ的概率密度函数的意义知：概率密度函数图象与x轴所围曲边梯形的面积即为随机变量在某区间取值的概率，由此将问题转化为计算定积分问题，利用微积分基本定理计算定积分即可

解答：解：由随机变量ξ的概率密度函数的意义知：
P(

1

4

＜ξ＜

1

2

)=

∫

1 2 1 4

（2x）dx=（x²）

|

1 2 1 4

=

1

4

-

1

16

=

3

16

故选 D

点评：本题考查了连续性随机变量概率密度函数的意义，连续性随机变量在某区间取值的概率的计算方法，定积分的意义及计算方法