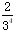题目内容
已知随机变量X的概率分布列为:P(X=k)=qk-1p(k=1,2,…,0<p<1,q=1-p),求证:EX=
证明:∵P(X=k)=qk-1p,
∵EX=1×p+2×qp+3q2p+…+kqk-1p+…
=p(1+2q+3q2+…+kqk-1+…)
令S=1+2q+3q2+…+kqk-1+(k+1)qk+…①
Sq=q+2q2+3q3+…+kqk+(k+1)qk+1+…②
①-②得:
S-Sq=1+q+q2+…+qk+…
即S(1-q)=![]()
∵S=![]()
∴EX=pS=p×![]() =
=![]() .
.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目